易坊好文馆

  1. 首页 > 玩科技 >

单位|复数背后的直觉——从数学游戏到现实世界( 三 )


文章图片

负的速度仅仅意味着物体在向相反的方向前进
虚数和复数
如果你已经理解了我们到目前为止所说的一切 ， 那么你已经可以预见我们将如何处理虚数的概念 。 考虑一下下面的方程 。
x^2 + 1 = 0
这一次 ， 无论是正数还是负数都无法解这个方程 。 让我们在我们的游戏中增加一些实体来玩 。 让我们定义一个新的符号i ， 是负1的平方根 。 为什么我们要这样定义一个符号呢？因为根据我们既定的游戏规则 ， 这可以解上面的方程 。 没有更深的含义 ， 就这么简单 。
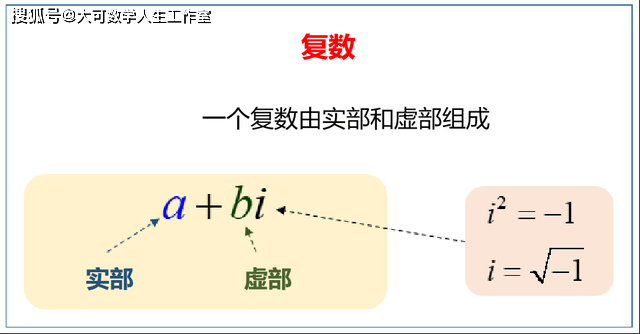
同样 ， 虚数可以使用与实数相同的代数规则进行加法和乘法 。 i+3i=4i ， i*i=-1 。 我们甚至可以将一个虚数与一个实数相加 ， 得到一个所谓的复数 。 在加法中使用的实数构成了复数的 "实部" ， 而虚数则构成了 "虚部" 。
单位|复数背后的直觉——从数学游戏到现实世界
文章图片

复数
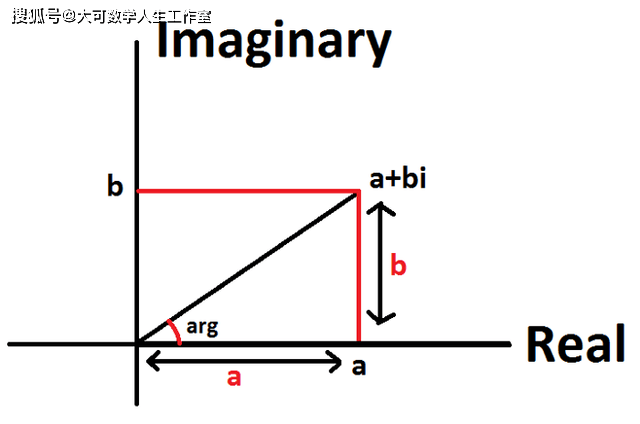
从几何学上讲 ， 就像实数一样 ， 我们可以用一条直线来形象化虚数 。 此外 ， 我们可以将虚线垂直于实线 ， 形成复数平面 ， 每个复数都对应着一个实坐标和一个虚坐标的点 。
单位|复数背后的直觉——从数学游戏到现实世界
文章图片

复数平面
好了 ， 我们已经成功地将虚数单位的概念纳入我们的游戏中 。 是时候找到一些应用和解释了 。
对于初学者来说 ， 复数在电气工程中一直被使用 。 它们是傅里叶变换的核心 ， 帮助我们分析特定信号的频率成分 。 此外 ， 在数学中 ， 包括复数在内的拉普拉斯变换帮助我们将微分方程转化为代数方程 ， 使其解更加简单 。 最后 ， 欧拉公式直接揭示了复数与余弦和正弦的联系 ， 因此 ， 当我们想描述任何类型的振荡时 ， 它们很容易被使用 。
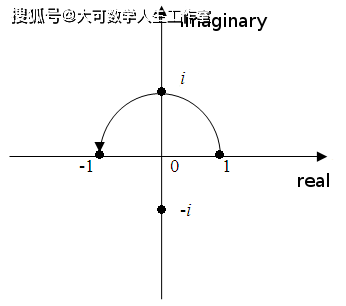
关于虚数的一个补充说明是 ， 我们可以把一个实数与虚数单位i的乘法看作是在复数平面内逆时针旋转90度 。
单位|复数背后的直觉——从数学游戏到现实世界
文章图片

i的乘法是复数平面内的旋转
以数字1为例 ， 考虑一下 。 这个数字与正实数一起位于右侧的实线上 。 1乘以i ， 你会得到数字i ， 从1的初始点旋转90度 。 再乘以i ， 我们会得到数字-1 ， 它再次位于实线上 。 再乘以2次 ， 我们又回到了开始的地方 。
复数在现实世界中的一个应用在量子力学中很明显 。 尽管我们不会在本文中深入研究薛定谔方程（感兴趣可以看这篇文章薛定谔方程 ， 从数学上看经典力学是如何产生量子物理学方程的） ， 但事实证明 ， 只有通过复数 ， 这个我们看似随意引入的概念 ， 我们才能准确地模拟在特定位置找到一个粒子的概率 。

推荐阅读


上一篇：电子|量子力学是如何撑起现代物理学的大厦的？

下一篇：运载火箭|加油，中国航天！航天科技集团2022将有40多次发射任务