exp|拓端数据tecdat:R语言普通最小二乘OLS，广义相加模型GAM ，样条函数逻辑回归_函数|进行|in|广义|optim|算法

原文链接：http://tecdat.cn/?p=21379
本文我们对逻辑回归和样条曲线进行介绍。
logistic回归基于以下假设：给定协变量x ， Y具有伯努利分布，

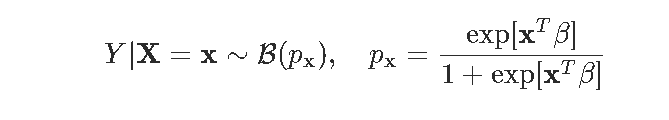
文章图片

目的是估计参数β 。
回想一下，针对该概率使用该函数是

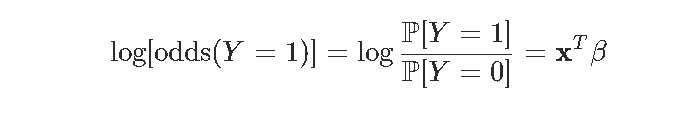
文章图片

（对数）似然函数
对数似然

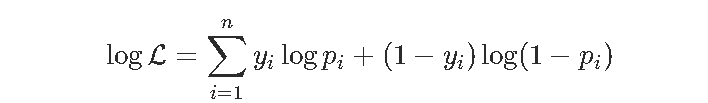
文章图片

其中。数值方法基于（数值）下降梯度来计算似然函数的最大值。对数似然（负）是以下函数

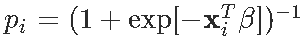
文章图片

negLogLik = function(beta){
-sum(-y*log(1 + exp(-(X%*%beta))) - (1-y)*log(1 + exp(X%*%beta)))
}

现在，我们需要一个起始点来启动算法
optim(par = beta_init, negLogLik, hessian=TRUE, method = "BFGS", control=list(abstol=1e-9))
在这里，我们得到

logistic_opt$par
(Intercept) FRCAR INCAR INSYS
1.656926397 0.045234029 -2.119441743 0.204023835
PRDIA PAPUL PVENT REPUL
-0.102420095 0.165823647 -0.081047525 -0.005992238

让我们在这里验证该输出是否有效。例如，如果我们（随机）更改起点的值会怎么样

plot(v_beta)
par(mfrow=c(1,2))
hist(v_beta[,1],xlab=names( )[ ])
hist(v_beta[,2],xlab=names( )[2])

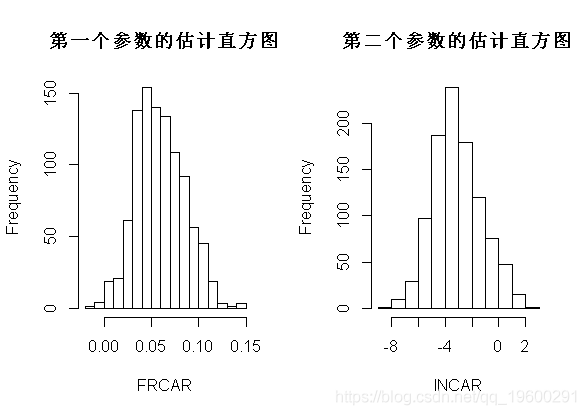
exp|拓端数据tecdat:R语言普通最小二乘OLS，广义相加模型GAM ，样条函数逻辑回归

文章图片

这里有个问题。注意，我们不能在这里进行数值优化。我们可以考虑使用其他优化方法

logLikelihoodLogitStable = function(vBeta, mX, vY) {
-sum(vY*(mX %*% vBeta - log(1+exp(mX %*% vBeta) +
(1-vY)*(-log(1 + exp(mX %*% vBeta))
optimLogitLBFGS = optimx(beta_init, logLikelihoodLogitStable,

最优点

文章图片

结果不理想。
我们使用的技术基于以下思想，

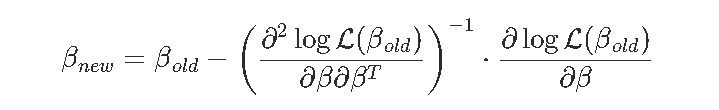
文章图片

问题是我的计算机不知道一阶和二阶导数。
可以使用这种计算的函数

logit = function(x){1/(1+exp(-x))}
for(i in 1:num_iter){
grad = (t(X)%*%(logit(X%*%beta) - y))
beta = beta - ginv(H)%*%grad
LL[i] = logLik(beta, X, y)

以我们的OLS起点，我们获得

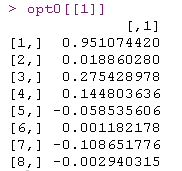
文章图片

如果我们尝试另一个起点

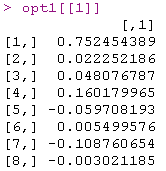
文章图片

一些系数非常接近。然后我们尝试其他方法。
牛顿（或费舍尔）算法
在计量经济学教科书里，您可以看到：

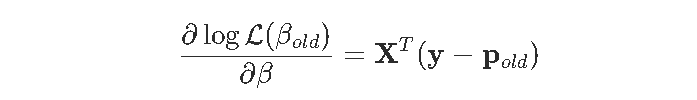
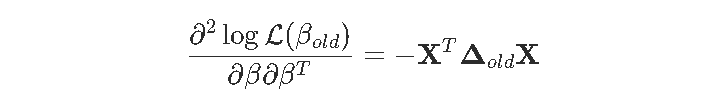
文章图片

beta=as.matrix(lm(Y~0+X)$coefficients
for(s in 1:9){
pi=exp(X%*%beta[,s])/(1+exp(X%*%beta[,s]))
gradient=t(X)%*%(Y-pi)
omega=matrix(0,nrow(X),nrow(X));diag(omega)=(pi*(1-pi))

在这里观察到，我仅使用该算法的十次迭代。

文章图片

事实是，收敛似乎非常快。而且它相当鲁棒，看看我们改变起点会得到什么

beta=as.matrix(lm(Y~0+X)$coefficients,ncol=1)*runif(8)
for(s in 1:9){
pi=exp(X%*%beta[,s])/(1+exp(X%*%beta[,s]))
gradient=t(X)%*%(Y-pi)
omega=matrix(0,nrow(X),nrow(X));diag(omega)=(pi*(1-pi))
Hessian=-t(X)%*%omega%*%X
beta=cbind(beta,beta[,s]-solve(Hessian)%*%gradient)}
beta[,8:10]

文章图片

效果提高了，并且可以使用矩阵的逆获得标准偏差。
标准最小二乘
我们更进一步。我们已经看到想要计算类似

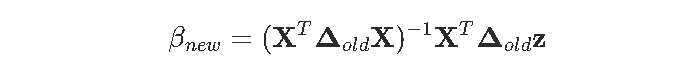
文章图片

但是实际，这是一个标准的最小二乘问题

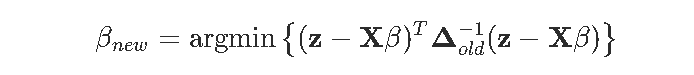
文章图片

这里唯一的问题是权重Δold是未知β的函数。但是实际上，如果我们继续迭代，我们应该能够解决它：给定β ，我们得到了权重，并且有了权重，我们可以使用加权的OLS来获取更新的β 。这就是迭代最小二乘的想法。
该算法

beta_init = lm(PRONO~.,data=https://www.sohu.com/a/df)$coefficients
for(s in 1:1000){
omega = diag(nrow(df))
diag(omega) = (p*(1-p))

输出在这里

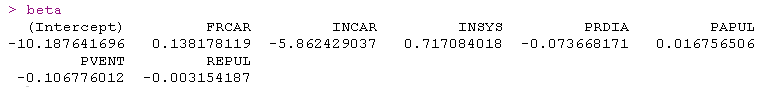
文章图片

结果很好，我们在这里也有估计量的标准差

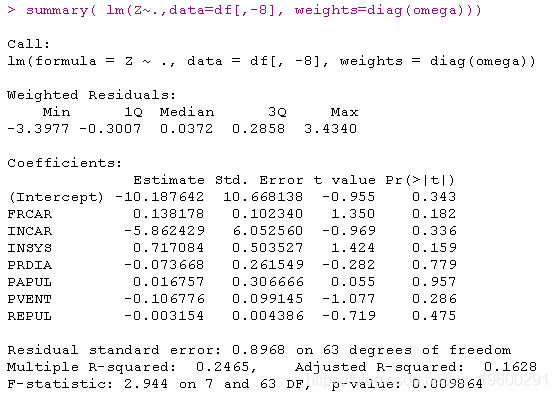
文章图片

标准逻辑回归glm函数：
当然，可以使用R内置函数

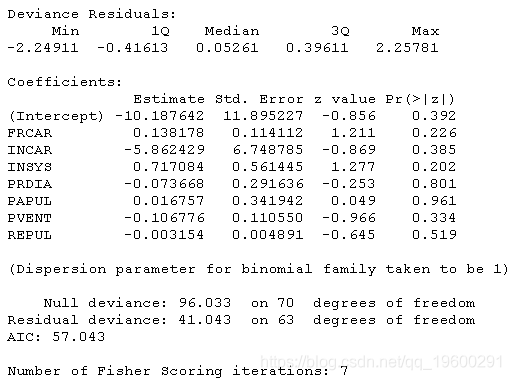
文章图片

可视化
让我们在第二个数据集上可视化从逻辑回归获得的预测

image(u,u,v ,breaks=(0:10)/10)
points(x,y,pch=19 )
points(x,y,pch=c(1,19)
contour(u,u,v,levels = .5

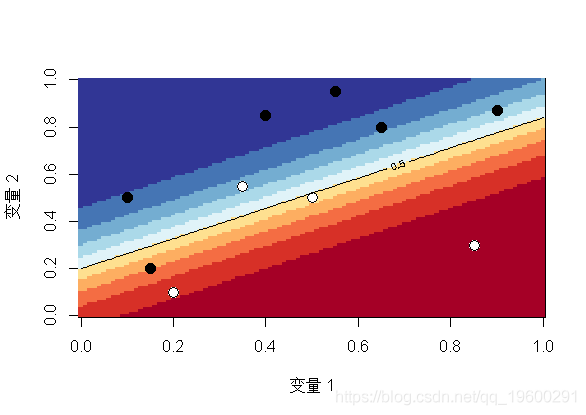
文章图片

这里的水平曲线-或等概率-是线性的，因此该空间被一条直线（或更高维的超平面）一分为二（0和1 ，生存和死亡，白色和黑色）此外，由于我们是线性模型，因此，如果更改截距（为创建两个类别的阈值），我们将获得平行的另一条直线（或超平面）。
接下来，我们将约会样条曲线以平滑那些连续的协变量。
分段线性样条函数
我们从“简单”回归开始（只有一个解释变量），我们可以想到的最简单的模型来扩展我们上面的线性模型，是考虑一个分段线性函数，它分为两部分。最方便的方法是使用正部函数（如果该差为正，则为x和s之间的差，否则为0）。如

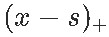
文章图片

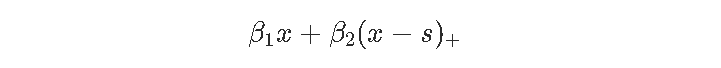
文章图片

是以下连续的分段线性函数，在s处划分。

文章图片

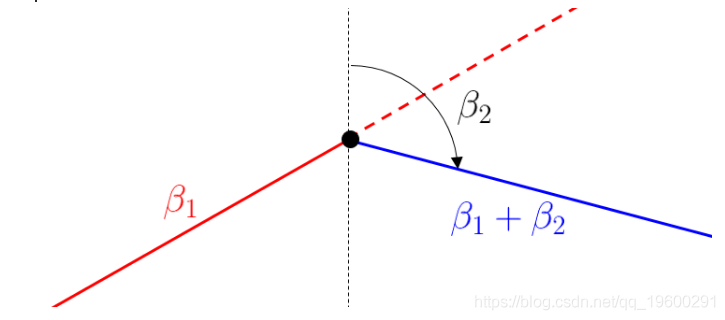
对于较小的x值，线性增加，斜率β1；对于较大的x值，线性减少。因此， β2被解释为斜率的变化。
当然，可以考虑多个结。获得正值的函数如下
pos = function(x,s) (x-s)*(x<=s)
然后我们可以在回归模型中直接使用它
回归的输出在这里

Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.1109 3.2783 -0.034 0.9730
INSYS -0.1751 0.2526 -0.693 0.4883
pos(INSYS, 15) 0.7900 0.3745 2.109 0.0349 *
pos(INSYS, 25) -0.5797 0.2903 -1.997 0.0458 *

因此，对于很小的值，原始斜率并不重要，但是在15以上时，它会变得明显为正。而在25以上，又发生了重大变化。我们可以对其进行绘图以查看发生了什么

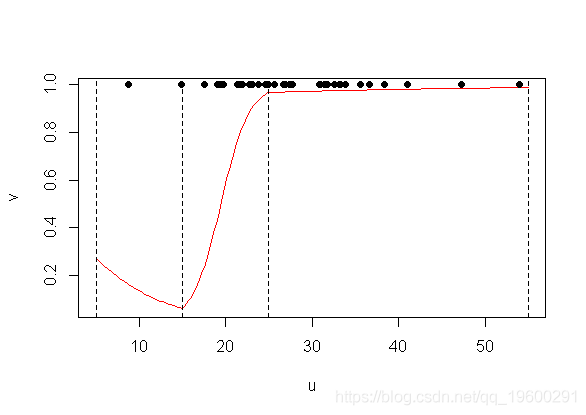
plot(u,v,type="l")
points(INSYS,PRONO)
abline(v=c(5,15,25,55)

文章图片

使用bs（）线性样条曲线
使用GAM模型，情况略有不同。我们将在这里使用所谓的 b样条曲线，
我们可以用边界结点（5,55）和结 {15,25}定义样条函数

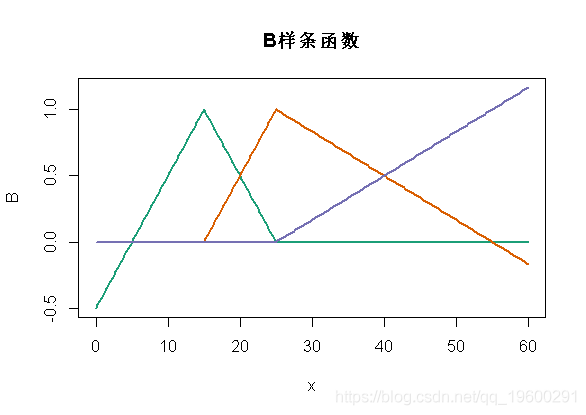
B = bs(x,knots=c(15,25),Boundary.knots=c(5,55),degre=1)
matplot(x,B,type="l",lty=1,lwd=2,col=clr6)

文章图片

如我们所见，此处定义的函数与之前的函数不同，但是在每个段（5,15）（15,25）和（25,55）。但是这些函数（两组函数）的线性组合将生成相同的空间。换个角度说，对输出的解释会不同，预测应该是一样的。

Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.9863 2.0555 -0.480 0.6314
bs(INSYS,..)1 -1.7507 2.5262 -0.693 0.4883
bs(INSYS,..)2 4.3989 2.0619 2.133 0.0329 *
bs(INSYS,..)3 5.4572 5.4146 1.008 0.3135

观察到像以前一样存在三个系数，但是这里的解释更加复杂了

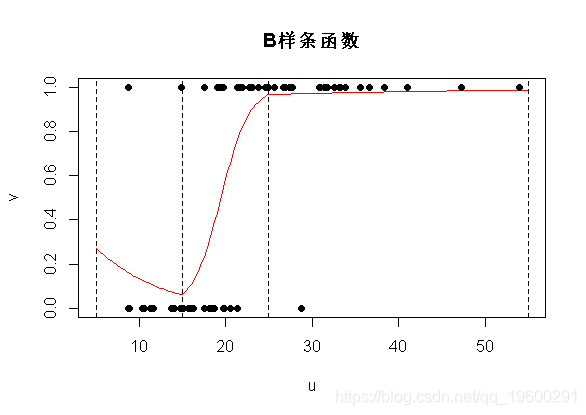
文章图片

但是，预测结果很好。
分段二次样条
让我们再往前走一步...我们是否也可以具有导数的连续性？考虑抛物线函数，不要对和进行分解，考虑对和进行分解。

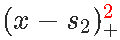
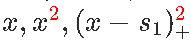
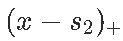
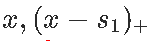
文章图片

Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 29.9842 15.2368 1.968 0.0491 *
poly(INSYS, 2)1 408.7851 202.4194 2.019 0.0434 *
poly(INSYS, 2)2 199.1628 101.5892 1.960 0.0499 *
pos2(INSYS, 15) -0.2281 0.1264 -1.805 0.0712 .
pos2(INSYS, 25) 0.0439 0.0805 0.545 0.5855

不出所料，这里有五个系数：截距和抛物线函数的三个参数，然后是中间两个附加项–此处（15,25）–以及右侧的部分。当然，对于每个部分，只有一个自由度，因为我们有一个抛物线函数（三个系数），但是有两个约束（连续性和一阶导数的连续性）。
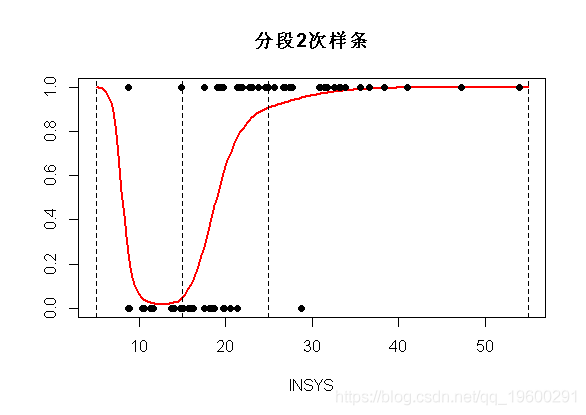
在图上，我们得到以下内容

文章图片

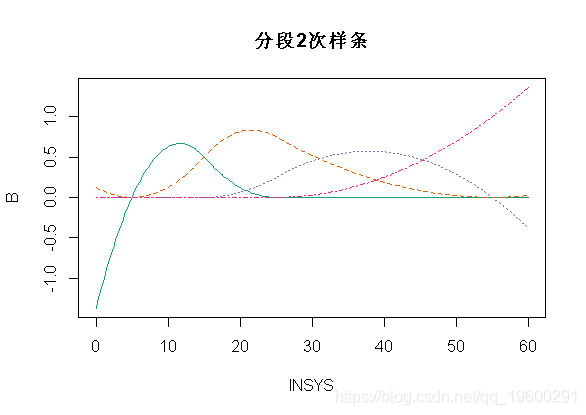
使用bs（）二次样条
当然，我们可以使用R函数执行相同的操作。但是和以前一样，这里的函数有所不同

matplot(x,B,type="l",col=clr6)

文章图片

如果我们运行R代码，得到

glm(y~bs(INSYS knots=c(15,25),
Boundary.knots=c(5,55),degre=2)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 7.186 5.261 1.366 0.1720
bs(INSYS, ..)1 -14.656 7.923 -1.850 0.0643 .
bs(INSYS, ..)2 -5.692 4.638 -1.227 0.2198
bs(INSYS, ..)3 -2.454 8.780 -0.279 0.7799
bs(INSYS, ..)4 6.429 41.675 0.154 0.8774

预测是完全相同的

plot(u,v,ylim=0:1,type="l",col="red")

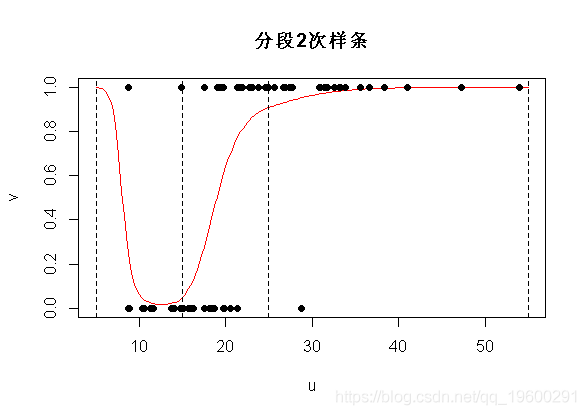
文章图片

三次样条
我们可以使用三次样条曲线。我们将考虑对进行分解，得到时间连续性，以及前两个导数的连续性。如果我们使用bs函数，则如下

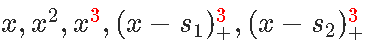
文章图片

matplot(x,B,type="l",lwd=2,col=clr6,lty=1
abline(v=c(5,15,25,55),lty=2)

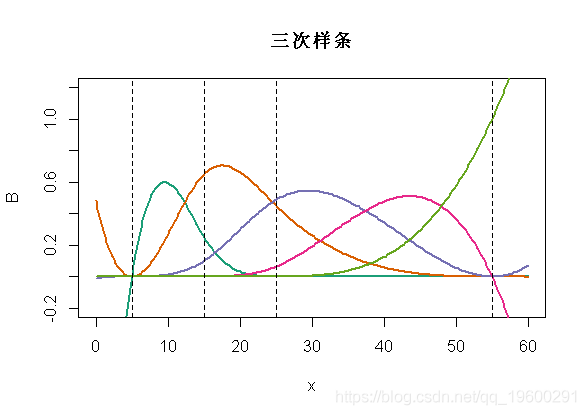
文章图片

现在的预测将是

bs(x,knots=c(15,25),
Boundary.knots=c(5,55),degre=3

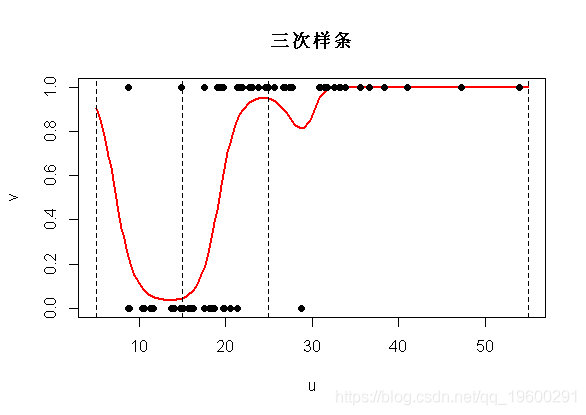
文章图片

结的位置
在许多应用程序中，我们不想指定结的位置。我们只想说（三个）中间结。可以使用
bs(x,degree=1,df=4)
可以查看

bs(x, degree = 1L, knots = c(15.8, 21.4, 27.15),
Boundary.knots = c(8.7, 54), intercept = FALSE)

它为我们提供了边界结的位置（样本中的最小值和最大值），也为我们提供了三个中间结。观察到实际上，这五个值只是（经验）分位数

quantile( ,(0:4)/4)
0% 25% 50% 75% 100%
8.70 15.80 21.40 27.15 54.00

如果我们绘制预测，我们得到
plot(u,v,ylim=0:1,type="l",col="red",lwd=2)

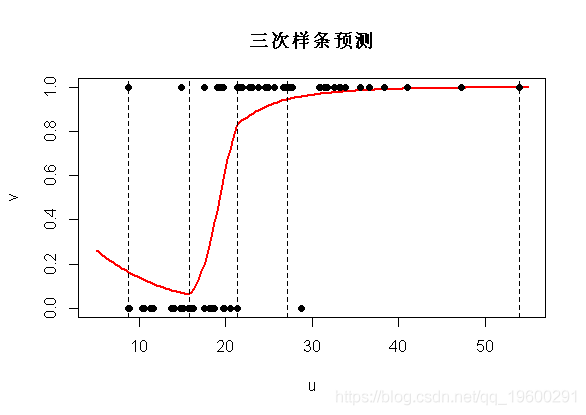
文章图片

如果我们回到logit变换之前的计算，我们清楚地看到断点是不同的分位数

plot(x,y,type="l",col="red",lwd=2)
abline(v=quantile(my ,(0:4)/4),lty=2)

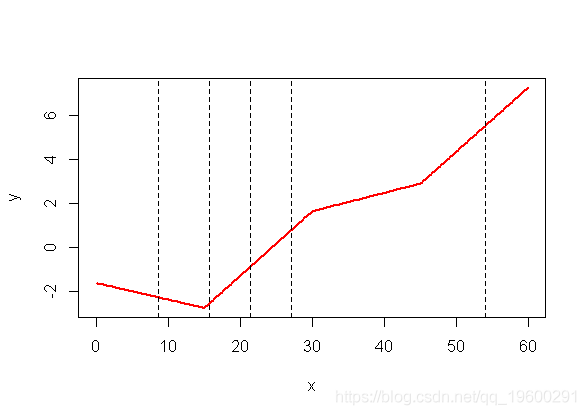
文章图片

如果我们没有指定，则不会得到任何结…

bs(x, degree = 2L, knots = numeric(0),
Boundary.knots = c(8.7,54), intercept = FALSE)

如果我们看一下预测
predict(reg,newdata=https://www.sohu.com/a/data.frame(u),type="response")
实际上，这和二次多项式回归是一样的（如预期的那样）

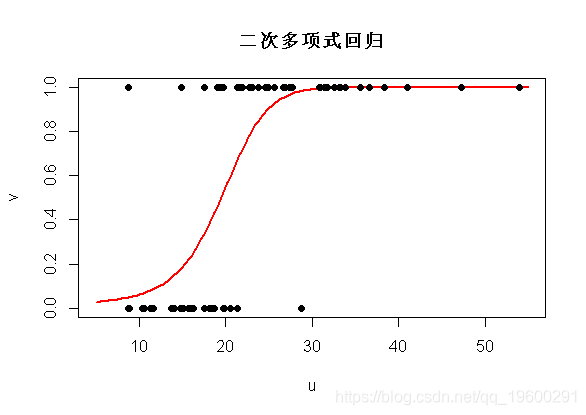
文章图片

相加模型现在考虑第二个数据集，包含两个变量。这里考虑一个模型

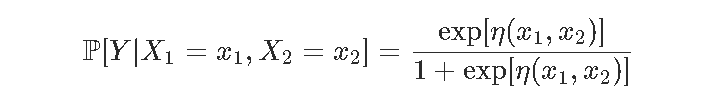
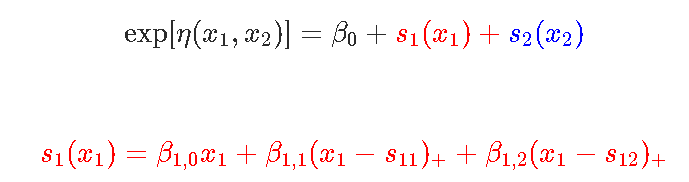
文章图片

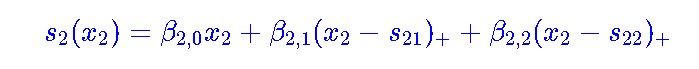
文章图片

然后我们用glm函数来实现相加模型的思想。

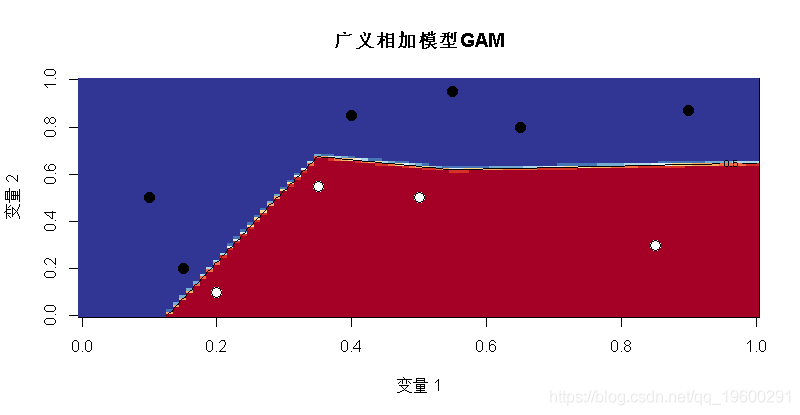
glm(y~bs(x1,degree=1,df=3)+bs(x2,degree=1,df=3), family=binomial(link =
v = outer(u,u,p)
image(u,u,v, ",col=clr10,breaks=(0:10)/10)

现在，我们能够得到一个“完美”的模型，所以，结果似乎不再连续

文章图片

persp(u,u,v,theta=20,phi=40,col="green"

文章图片

当然，它是分段线性的，有超平面，有些几乎是垂直的。
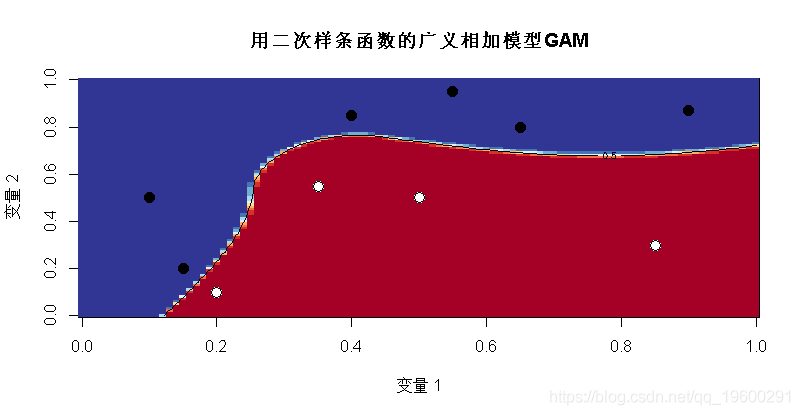
我们也可以考虑分段二次函数

contour(u,u,v,levels = .5,add=TRUE)

文章图片

有趣的是，我们现在有两个“完美”的模型，白点和黑点的区域不同。
在R中，可以使用mgcv包来运行gam回归。它用于广义相加模型，但这里只有一个变量，所以实际上很难看到“可加”部分，可以参考其他GAM文章。

文章图片

最受欢迎的见解
1.R语言多元Logistic逻辑回归应用案例
2.面板平滑转移回归(PSTR)分析案例实现
3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）
4.R语言泊松Poisson回归模型分析案例
5.R语言回归中的Hosmer-Lemeshow拟合优度检验
6.r语言中对LASSO回归， Ridge岭回归和Elastic Net模型实现
7.在R语言中实现Logistic逻辑回归
8.python用线性回归预测股票价格
【exp|拓端数据tecdat:R语言普通最小二乘OLS，广义相加模型GAM ，样条函数逻辑回归】9.R语言如何在生存分析与Cox回归中计算IDI ， NRI指标