文章图片
通过学习边的连接 , 逻辑层便可以灵活地表示有着合取或析取范式形式的离散分类规则 。 然而问题在于 , 虽然离散的逻辑层可解释性好 , 但自身不可导 , 难以训练 , 这也是为什么还需要一个对应的连续版本的逻辑层 。
连续逻辑层
连续逻辑层必须是可导的 , 并且当二值化连续逻辑层的参数时 , 可以直接得到它相对应的离散逻辑层 。 为此需要:
- 将 0/1 邻接矩阵替换为 [0, 1] 之间的实数权重矩阵
- 用逻辑激活函数替换逻辑运算
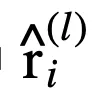
文章图片
和
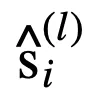
文章图片
分别为连续合取层和连续析取层中的节点 。
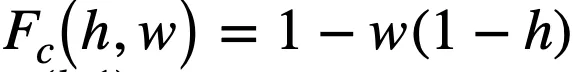
文章图片
而
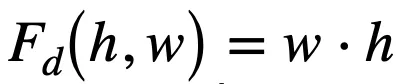
文章图片
, 二者通过
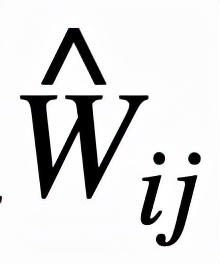
文章图片
的大小来决定
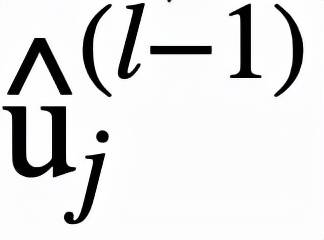
文章图片
对最终结果的影响的大小 。
如果
=0 , 则
对最终结果没有影响 。
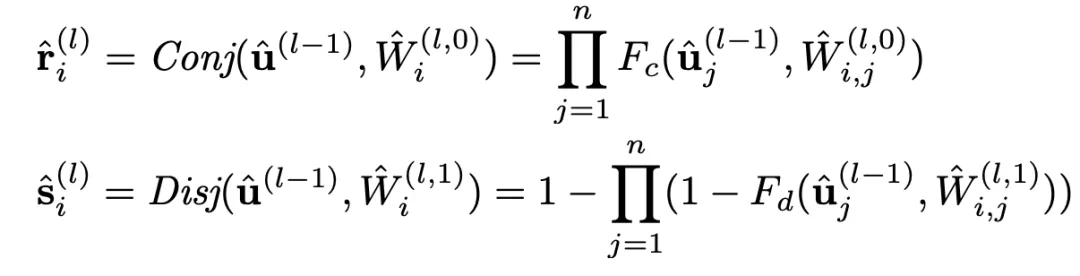
文章图片
虽然这两个逻辑激活函数能够较好地用可导的实数运算模拟逻辑运算 , 但其存在严重的梯度消失问题 , 无法处理特征数较多的情况 , 可扩展性较差 。 分析逻辑激活函数
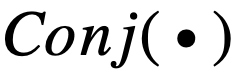
文章图片
和
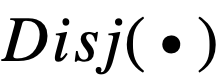
文章图片
以及相应的导数可以发现 , 使用连乘来模拟逻辑运算是导致梯度消失的主要原因 。
以
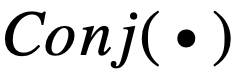
文章图片
为例 , 其对应导数如下:
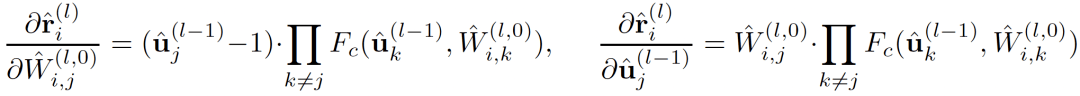
文章图片
由于

文章图片
, 则当相乘的
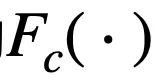
文章图片
数量较多时(一般指特征数较多或节点数较多) , 导数结果都会趋向于 0 , 即出现了梯度消失的问题 。
推荐阅读
- 星链|石豪:在太空,马斯克和美国当局是如何作恶的
- 下架|APK Installer 和 WSATools 同时躺枪:冒牌应用登陆微软应用商店
- 影像|iQOO 9 系列预热:首发三星 GN5 传感器,150° 鱼眼超广角
- 软件和应用|AcrylicMenus:让Windows 10右键菜单获得半透明效果
- 技术|使用云原生应用和开源技术的创新攻略
- 软件和应用|iOS/iPadOS端Telegram更新:引入隐藏文本、翻译等新功能
- 实力比|小米12对标苹果遭嘲讽?雷军:国产手机的实力比想象中强,有和苹果比较的勇气
- Apple|法官称苹果零售店搜包和解协议虽不完美,但可继续进行
- 部落|excel固定显示行列视频:应用冻结窗格同时固定标题行和列
- 最新消息|宝马LG和其他公司正考虑使用量子计算机解决具体问题







