因此 , 微积分可分为两个步骤:切分和重组 。 用数学术语来说 , 切分过程叫作微分学 。 重组过程叫作积分学 。
现在 , 我们终于可以阐明这个伟大的理念了 。
无穷原则
为了探究任意一个连续的形状、物体、运动、过程或现象(不管它看起来有多么狂野和复杂) , 把它重新想象成由无穷多个简单部分组成的事物 , 分析这些部分 , 然后把结果加在一起 ,就能理解最初的那个整体 。
而这一切的难点就在于 , 我们需要和无穷打交道 , 但无穷是微积分中最令人头疼的问题 , 它往往会挣脱主人的控制 , 不可避免地会攻击创造出它们的人 。
微积分的创造者意识到了这种危险 , 但仍然发现无穷的魅力不可抗拒 。 当然 , 它偶尔也会发狂 , 带来悖论、困惑和哲学灾难 。 不过 , 数学家每次都能成功地征服无穷怪物 , 理顺它的行为 , 让它重回正轨 。 驾驭无穷并利用它的力量 , 这种欲望是一条贯穿微积分的2500年历史的叙事线索 。
03
曲线、运动和变化
无穷原则围绕着方法论主题构建了微积分的故事 。 但微积分既与方法论有关 , 也与谜题有关 。 最重要的是 , 有三个谜题促进了微积分的发展 , 它们分别是曲线之谜、运动之谜和变化之谜 。
一切都始于曲线之谜 。
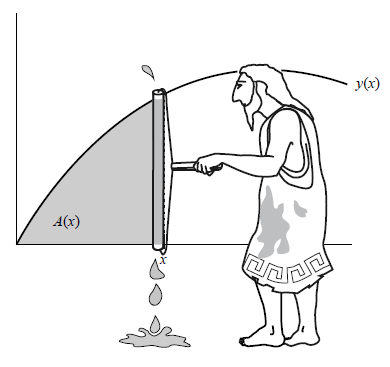
没有人能算出一个球体的表面积或体积有多大 , 即使是求圆的周长和面积 , 在古代也是一个难题 。 人们既不知道该从何处着手 , 也找不到便于理解的平直部件 。 总之 , 所有弯曲的东西都难以捉摸 。
微积分就是在这样的背景下诞生的 , 它萌生于几何学家对圆度的好奇心和挫败感 。 圆、球体和其他曲线形状是他们那个时代的“喜马拉雅山脉” , 它们激发了人类的冒险精神 。 就像攀登珠穆朗玛峰的探险家一样 ,几何学家之所以想解决曲线问题 , 是因为它们就在那里 。
文章图片
有些几何学家坚持认为“曲线事实上是由平直部件构成的” , 这种观点带来了突破性进展 。 尽管这不是事实 , 但我们可以假装它是真的 。 那么 , 唯一的问题就在于 , 这些部件必须无穷小 , 而且数量无穷多 。 通过这个巧妙的构思 , 积分学诞生了 , 这是人们对无穷原则的最早应用 。 多个世纪以来 , 世界上最伟大的数学家都在努力探究这个难题的解决办法 。 不过 , 通过共同的努力(有时还伴有激烈的竞争) , 他们终于在破解曲线之谜上取得了进展 。
文章图片
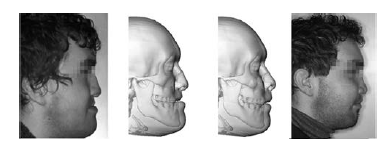
用微积分原理绘制的需下颌手术的患者面部模型(左二)和预测术后效果模型(右二)
推荐阅读
- 最新消息|世界单体容量最大漂浮式光伏电站在德州并网发电
- 最新消息|中围石油回应被看成中国石油:手续合法 我们看不错
- 硬件|汽车之家年底裁员,员工称多个职能部门已被撤销
- 四平|智慧城市“奥斯卡”揭晓!祝贺柯桥客户荣获2021世界智慧城市治理大奖
- 换卡|突然宣布:被迫停止运营!
- 系列|2021中国航天发射圆满收官!年发射55次居世界第一
- 视点·观察|张庭夫妇公司被查 该怎样精准鉴别网络传销?
- 社交|Facebook被指试图在美政客中抹黑前雇员Frances Haugen声誉
- IT|新能源汽车年底卖爆 展车都被抢购 咋回事?
- 科技创新平台|云南:打造世界一流食用菌科技创新平台







