易坊好文馆

  1. 首页 > 玩科技 >

检测|基于双目视觉的目标检测与追踪方案详解( 二 )


检测|基于双目视觉的目标检测与追踪方案详解
文章图片

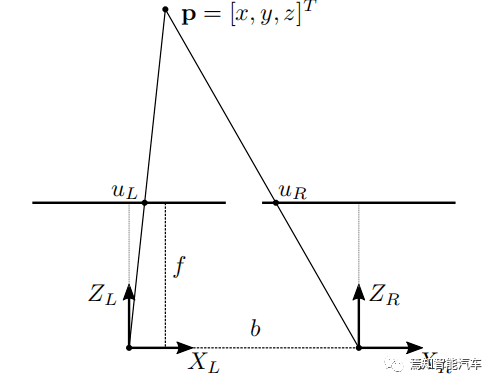
图2 简单的相机视差模型
光学中心也相距一定距离 b ， 这被称为立体基线 ， 则视差计算方法如下：
（4）
计算水平和垂直坐标 x 和 y 依赖于与以前相同的原则 。 然而 ， 深度信息具有唯一确定性 ， 其过程就是求解环境检测点 p 的 z 坐标 。 其中 uL和 uR是点 p 投影到相应图像平面上的左右水平坐标 。 假设坐标系的原点与左相机中心重合 ， 则
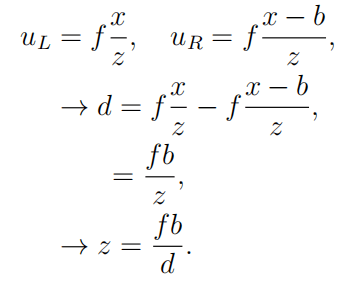
检测|基于双目视觉的目标检测与追踪方案详解
文章图片

（5）
等式 (5) 给出了理想水平立体配置中校准相机的视差和范围之间的关系 ， 深度计算所需的关键量是视差 ， 确定视差依赖于找到相应的像素在相应的图像中的位置点 ， 对应的方法一般是依靠纹理信息进行帧间匹配 。
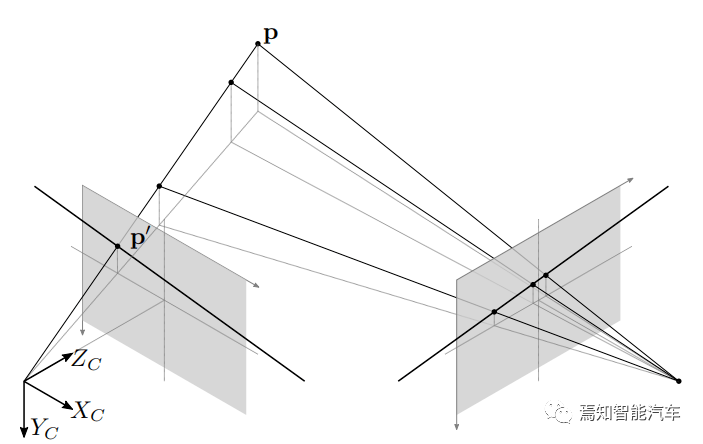
实际上 ， 通过物理排列来实现完美的相机对准是不可能的 。 两个相机之间的一般对齐方式如下图所示 。 点 p 投影到左侧相机图像平面上的点 p’ 。 这个点在右图像平面上的对应关系被限制在平面上绘制的水平基线上 。 事实上 ， 任何投影到左相机平面绘制线上的点都被限制为与右图像平面上的相应线重合 。 这些线被称为共轭极线 ， 两幅图像中各自的图像点在该极线上应该满足对极约束条件 ， 它们用于指导立体图像点对应的搜索过程范围 。
检测|基于双目视觉的目标检测与追踪方案详解
文章图片

图3 立体视觉测量提取算法示意图
对极约束的数学形式简单明了 ， 我们可以看出 ， 只要我们能够找出两幅图像之间的多组特征点关系 ， 就可以根据对极约束求出两幅图像之间的运动关系 。
接下来从数学角度描述一下对极约束 。
根据针孔相机模型,我们知道空间位置点P 在相机中的像素位置为p1 ， p2。 这里 K 为相机内参矩阵,R, t 为两个坐标系的相机运动(如果我们愿意,也可以写成代数形式) 。 如果使用齐次坐标,我们也可以把上式写成在乘以非零常数下成立的等式：
现在 ， 取:
这里的 x1 , x2 是两个像素点的归一化平面上的坐标 。 代入上式 ， 得:
两边同时乘以t的转置矩阵t^ ， 相当于两侧同时对t做外积：
然后 ， 两侧同时乘以 ， 那么
如上等式左侧 ，t^x2是一个与t和x2都垂直的向量（相当于对t和x2形成的平面做一条法线） ， 把它再和x2做内积时 ， 将得到0 ， 因此 ， 我们得到一个简洁的对极约束式子：
重新带入p1 ， p2 ， 得到另外一种表示形式
我们把对极约束数学表达式中的中间部分记为两个矩阵：基础矩阵(Fun-damental Matrix)F 和本质矩阵(Essential Matrix)E ， 可以进一步简化对极约束:

推荐阅读


上一篇：纵向|华为京东超级品牌日开启，时尚达人不要错过华为P50宝盒！

下一篇：都蛮|宝盒 P50 Pocket正式发布了，这上手效果可以吧？