易坊好文馆

  1. 首页 > 玩科技 >

检测|基于双目视觉的目标检测与追踪方案详解( 五 )


对于测量和的过程中 ， 前面提到校准问题被转换为优化问题 ， 优化程序的任务是通过改变构成外部校准的参数来最小化误差函数 。 从稀疏特征跟踪框架中获取的时空信息用于识别运动图像区域 。 外观信息被完全忽略 ， 因此不会产生特定于对象的结果 。 如下图显示了测量提取算法的基本工作流程 ， 可以概括如下：稀疏特征检测器识别随后跟踪的强候选特征 。 跟踪器的过滤需要引入平滑策略 ， 实现基本的异常值去除 ， 并为轨迹存储和分析提供框架 。 可用信息最终在聚类例程中进行处理 ， 该例程需要对相似的特征轨迹进行分组 。
立体视觉测量提取算法示意图
1）特征提取
特征检测通常是使用加速段测试 (FAST) 算法中的特征检测进行的 ， 该检测器在计算复杂性方面明显优于其他替代方案 ， 并且专为一致性高的多视图特征提取而量身定制 ， 这些属性有利于将 FAST 角点检测器用于在实时立体视觉中的应用 。
使用稀疏特征检测有一些固有的缺点 ， 其中最值得注意的是无法从低纹理图像区域收集信息 ， 这可能会阻碍最终准确估计目标范围的能力 。 范围信息应主要从视觉子系统中提取 ， 因为它提供比雷达更高的分辨率 。 为了减轻可能的负面影响 ， 设置特征检测阈值以产生半密集信息 ， 即分布在视野中的数千个特征被识别为跟踪候选 。 通过这种方法 ， 可以获得相当准确的范围信息 ， 而计算需求仍然比密集检测方法低得多 。
2）特征追踪
算法运行所需的时间数据可通过状态估计器获得 ， 该估计器随时间跟踪检测到相应的特征 ， 由此产生的运动信息对于运动物体分割具有重要价值 。 本文将详细介绍实现的特征跟踪框架 。
①卡尔曼滤波器
检测目标的半密集性要求对后续处理进行仔细考虑 ， 可能数以千计的跟踪特征需要非常有效的状态估计器 。 为此 ， 引入了卡尔曼滤波器 。 卡尔曼滤波器是贝叶斯滤波器递归方程的可实现公式 ， 要素不是传播完整的目标状态密度 ， 而是采用高斯分布进行近似 ， 即
（9）
其中 N (x; m, P) 表示在具有均值 m 和协方差 P 的向量 x 上定义的高斯分布 。 卡尔曼滤波器递归方程的一个重要约束是它必须保留状态分布的高斯结构 。 这意味着动态和测量模型必须是线性高斯变换 。 请注意 ， 在传统控制系统中发现的控制输入不包括在预测更新中 ， 因为该数量在目标跟踪中是未知的 。 对于线性模型 ， 以下方程定义了卡尔曼滤波器的预测正确递归：
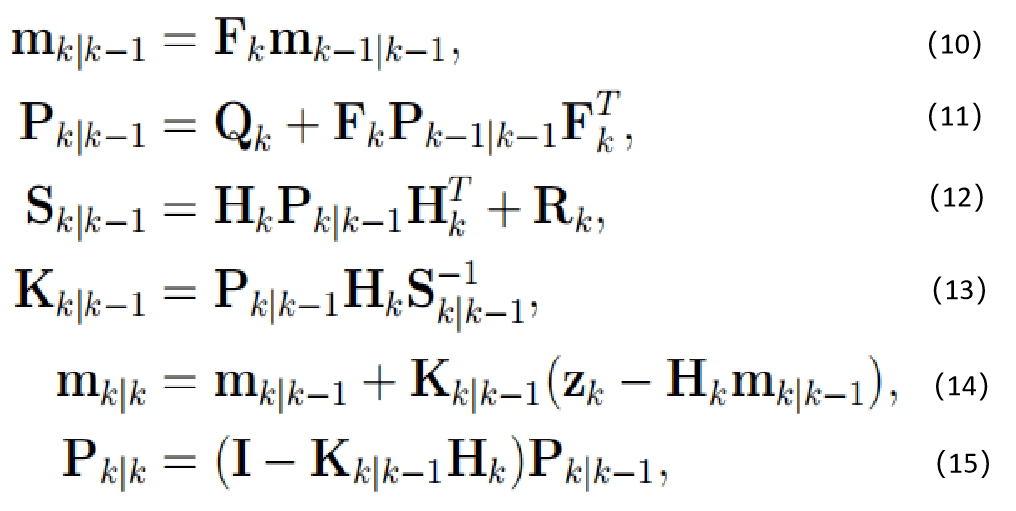
检测|基于双目视觉的目标检测与追踪方案详解
文章图片

其中 Fk 是状态转移矩阵 ， Qk 是过程噪声协方差 ， Hk 是观测矩阵 ， Rk 是测量噪声协方差 。 等式（11）和（12）定义了预测更新 ， 而等式（13）到（15）使用相关联的测量zk定义了测量更新日期 。 预测更新本质上是通过 Fk 和 Qk 描述的线性动态模型对状态分布的变换 。 转移矩阵描述了 k -1 时刻的状态均值与 k 时刻的先验之间的确定性关系 ， 而过程噪声协方差矩阵则对转移中的不确定性进行建模 。 在目标跟踪中 ， 这些矩阵来源于目标的运动模型 ， 测量更新结合了观察来改进状态估计 ， 这里的关键量是测量预期测量更新值 Hkmk|k-1与实际测量值Z k的差值 ， 更新协方差由矩阵 Sk|k?1给出 。 该创新及其协方差通过卡尔曼增益 Kk|k-1影响方程（15）中的结果更新 。

推荐阅读


上一篇：纵向|华为京东超级品牌日开启，时尚达人不要错过华为P50宝盒！

下一篇：都蛮|宝盒 P50 Pocket正式发布了，这上手效果可以吧？