易坊好文馆

  1. 首页 > 玩科技 >

检测|基于双目视觉的目标检测与追踪方案详解( 六 )


对于小状态向量维数 ， 卡尔曼滤波器为贝叶斯状态估计提供了一个非常有效的框架 ， 因为它的递归方程仅依赖于简单的矩阵乘法 。 非线性动态和测量模型可以通过将非线性变换近似为高斯来合并 。 泰勒级数展开和无迹变换分别表征扩展卡尔曼滤波器和无迹卡尔曼滤波器 ， 其中两个是卡尔曼滤波器最常见的非线性扩展 。
②状态空间模型
图像特征的测量在图像坐标中可用 ， 但在惯性坐标中需要 DATMO 上下文中的目标轨迹 。 使用图像平面测量在惯性空间中进行跟踪将需要非线性近似技术 ， 然而 ， 非线性估计方法的实现将显著增加跟踪器的计算需求 。 在最优性和速度之间的权衡中 ， 后者被选择用于稀疏特征跟踪 ， 即在图像坐标中跟踪特征 ， 这使得能够使用标准线性卡尔曼滤波器 。 由于加速坐标系 ， 实际上图像坐标不是惯性坐标可能会导致奇怪的非线性效应 ， 因此线性卡尔曼滤波器是一个近似值 。
接下来 ， 布局特征跟踪器的动态和测量模型 。 每个特征点的运动是根据恒速模型使用线性动力学和高斯噪声建模的
（16）
其中 u 是特征的水平图像坐标 ，vu是其速度 ，σw是加速度噪声标准偏差 ， ΔT 是时间步长 。 对于构成图像坐标的其余轴 ， 即垂直坐标 v 和视差 d ， 实现了精确解耦跟踪器 。 因此假设各个图像平面尺寸是完全独立的 ， 由于必须反转的矩阵的维数较小 ， 因此解耦的低阶卡尔曼滤波器更有效 ， 可以通过使用 OpenCV 的立体块匹配密集立体对应算法来合并视差信息 。 尽管每个特征的差异搜索有望提高效率 ， 但额外的研究工作是不必要的 。 在这里 ， 差异仅需要作为概念证明 。 因此 ， 仅从左侧图像中提取特征 ， 并且可以从密集对应算法中获得相应的视差 。
特征跟踪测量模型也是线性的 ， 形式为
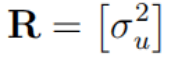
检测|基于双目视觉的目标检测与追踪方案详解
文章图片

（17）
其中 σu是水平维度中测量噪声的标准偏差 ， 相同的更新矩阵适用于其他维度 ， 基于创新的异常值拒绝策略被纳入特征跟踪框架 ， 如果创新大于创新协方差平方根的常数因子标准偏差 ， 即
（18）
其中 c 是一个常数 ， 然后删除轨道 。 此规则在所有三个跟踪维度中都实施 ， 如果有任何未通过测试 ， 则删除该跟踪 。 请注意 ， 如上方程中的数量减少为长度为 1 的向量和 1 × 1 矩阵 ， 即它们是标量 。 在除了基于异常值的轨道删除 ， M/N 逻辑规则也可用于轨道管理 。
选择线性图像平面状态空间模型的结果是 ， 由于底层特征的框架和跟踪框架不同 ， 可能会导致加速效应 。 虽然并不理想 ， 但跟踪器会产生轨道平滑效果并允许简单的异常值去除 ， 同时将计算开销降至最低 。

推荐阅读


上一篇：纵向|华为京东超级品牌日开启，时尚达人不要错过华为P50宝盒！

下一篇：都蛮|宝盒 P50 Pocket正式发布了，这上手效果可以吧？