一、试题呈现
定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角 , 称为该三角形第三个内角的遥望角.
(1)如图1,∠E是?ABC中∠A的遥望角.若∠A=α , 请用含α的代数式表示∠E;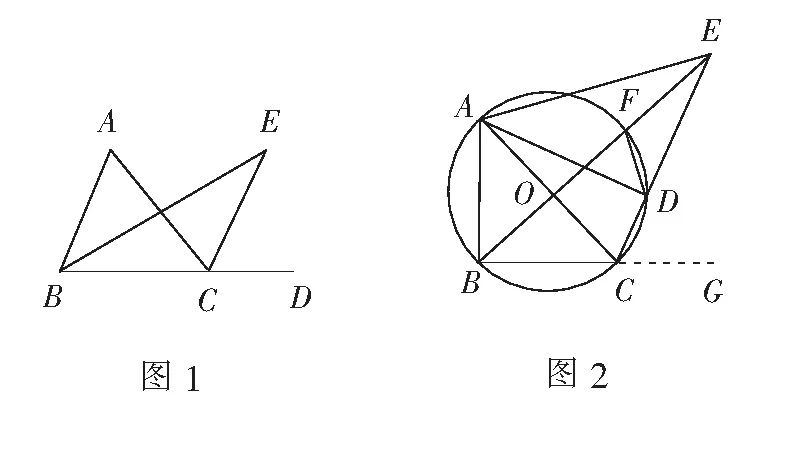
(2)如图2,四边形ABCD内接于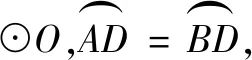
四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是?ABC中∠BAC的遥望角;
(3)如图3,在(2)的条件下 , 连结AE,AF,若AC是⊙O的直径.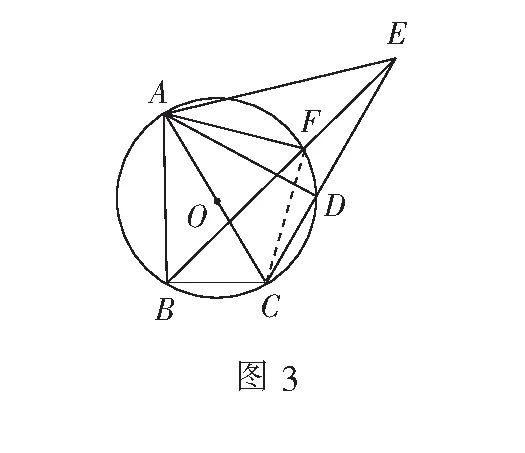
① 求∠AED的度数;
② 若AB=8,CD=5,求?DEF的面积.
二、解法赏析
(1)思路1 三角形外角定理由遥望角定义以及三角形外角定理 , 可得
∠E=∠ECD-∠EBD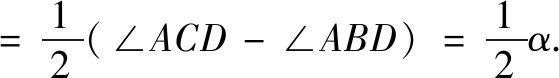

思路2 圆周角定理
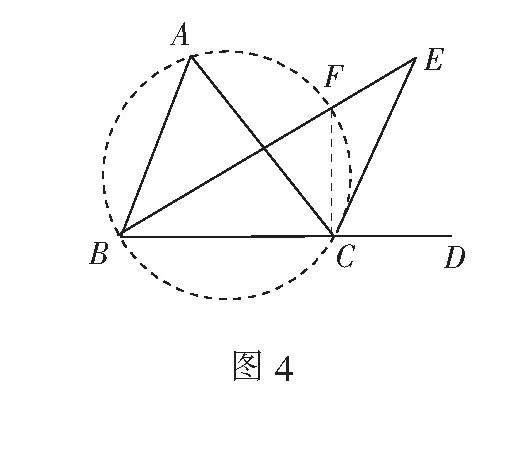
如图4 , 画出?ABC的外接圆,BE与这个圆的交点为F , 连结CF.
由遥望角定义,得∠ACE=∠ECD,
即∠ACF+∠FCE=∠E+∠EBC
由圆周角定理 , 得
∠ACF=∠ABF=∠EBC,
∴∠FCE=∠E.
又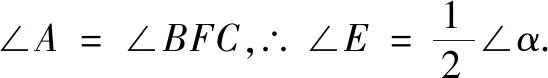
(2)如图2 , 延长BC至点G.
∵四边形BCDF内接于⊙O ,
∴∠EDF=∠FBC.
又∠EDF=∠ADF,∴∠FBC=∠ADF.
∵∠ABF=∠ADF , ∴∠ABF=∠FBC.
∵四边形ABCD内接于⊙O ,
∴∠ECG=∠BAD ,
又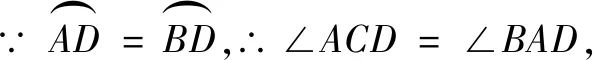
∴∠ECG=∠ACD.
故∠BEC是?ABC中∠BAC的遥望角.
(3)①如图3 , 连结CF , 则∠BAC=∠BFC.
由(2) , 可知∠BAC=2∠BEC ,
∴∠BEC=∠FCD , 即FC=FE.
∵AC是⊙O直径 ,
∴∠ABC=∠AFC=90°.又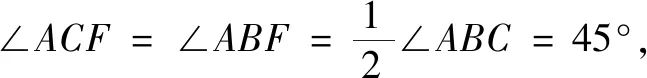
∴AF=FC.∵FC=FE,∴AF=FE.
故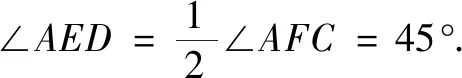
②虽然题中条件AB=8 , CD=5与?DEF没有直接关系 , 但由① , 可知DE=AD , 且AD是圆中的弦.因此 , 我们可从线段AD入手.
【数学|巧建构多视角明导向-这道中考数学题值得研究】
思路1 相似法1
如图5 , 连结CF , 过点A作AG⊥BE于点G , 过点F作FM⊥CE于点M.
∵AC是⊙O的直径 , BE平分∠ABC ,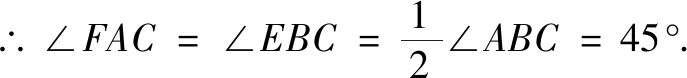
由① , 可知∠AED=45°,
∴∠AED=∠FAC.易证∠AEG=∠CAD,
∴?EGA∽?ADC,则有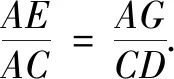
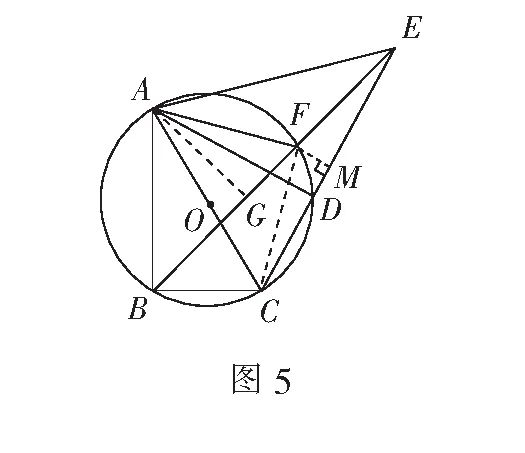
在等腰Rt?ABG中 , AB=8 ,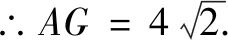
又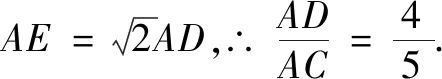
在Rt?ADC中 , CD=5 ,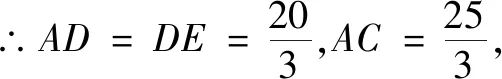
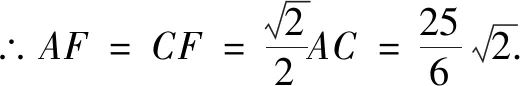
过点F作FM⊥CE于点M , 则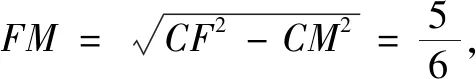

思路2 相似法2
如图6 , 连结BD , 则由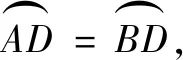
得AD=BD.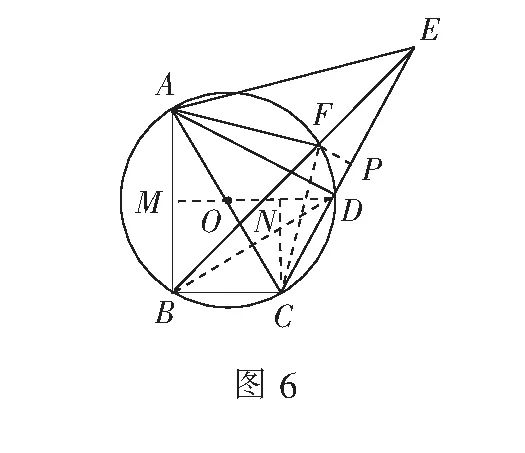
连结DO , 并延长交AB于点M , 则AM=BM=4.过点C作CN⊥DM于点N , 则四边形BCNM为矩形 ,
∴CN=BM=4.在Rt?CND中 , CD=5 ,
∴DN=3.∵∠ADN+∠CDN=90°,∠CDN+∠NCD=90°,∴∠ADN=∠NCD,
∴Rt?AMD∽Rt?DNC.
则有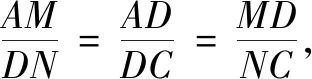
即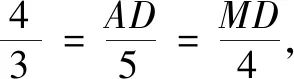
解得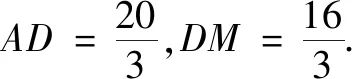

思路3 代数法
如图7 , 设AE交⊙O于点H.连结BD , HB , HC , HD , HO , 并延长HO交BC于点Q.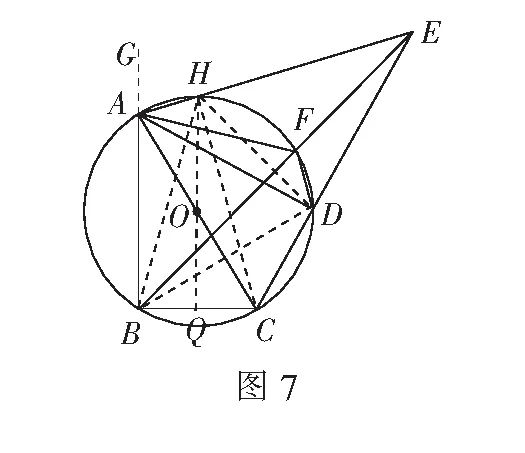
由(2)和(3)① , 可得∠BAC=2∠BEC , ∠ACB=2∠AEB.
易证BD=DE=AD , HB=HE=HC.
设BD=DE=AD=x,HB=HE=HC=y,⊙O的半径为r.
在Rt?ADC,Rt?EHC和Rt?HCQ中 , 52+x2=(2r)2,
①y2+y2=(5+x)2,
②(4+r)2+(r2-42)=y2.
③由① , ② , ③ , 解得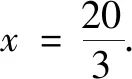

三、试题解读
1.“构建新定义”源于教材 , 重基础
命题的过程就是“选材—重构—应用”知识的过程.本试题源于教材探索研究栏目.
原题 (1)如图8 , 在?ABC中 , ∠ABC , ∠ACB的平分线相交于点O , ∠A=40°,求∠BOC的度数.
(2)如图9 , ?A′B′C′的两个外角∠C′B′D,∠B′C′E的平分线相交与点O′ , ∠A′=40° , 求∠B′O′C′的度数.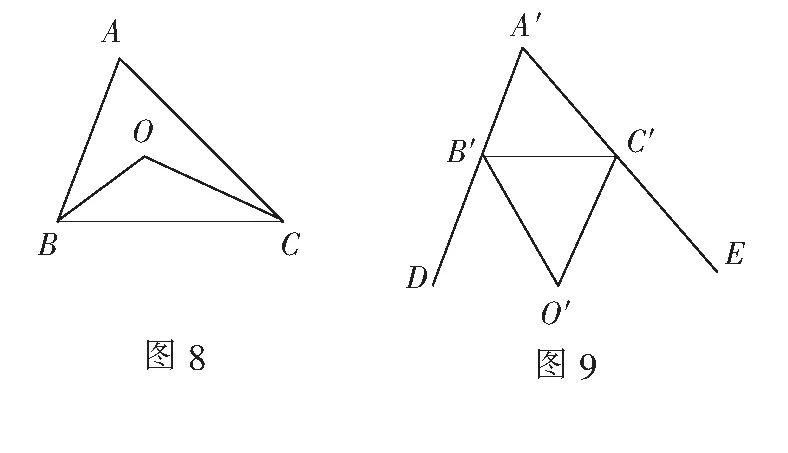
(3)由(1) , (2) , 可以发现∠BOC与∠B′O′C′之间有怎样的数量关系?若∠A=∠A′=n° , ∠BOC与∠B′O′C′之间是否还具有这样的关系 , 为什么?
教材原题是探索两个内角和两个外角平分线组成的新角与第三个内角间的数量关系.相对比 , 试题探索“一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角”与第三个内角间的数量关系,并将该关系进行综合应用.命题者根据教材内容和学情,以课程标准为基准,与考情相相合,源于教材 , 又异于教材,将知识点进行整合.
2.“判定新图形”源于本质,显学力
学力是一个人知识水平以及接受知识、理解运用知识的能力.中考题不仅仅考查学生的知识掌握情况,更注重考查学生应用知识解决问题的能力.
试题给出一个新图形定义,旨在探究新图形的性质与判定以及与已有知识之间的联系,以此反馈学生对图形学习方法的掌握情况.
试题的命制力避模型化套路,注重问题本质与通性通法,淡化特殊技巧,有效地检测了学生数学学习的能力.
3.“综合应用题”考查素养,重育人
“学会”是应试教育的终点;“会学”是培养学生核心素养的起点.
试题通过三个有梯度的问题来理解和应用新定义.学生在掌握新定义的过程中,利用一个角与它遥望角之间的二倍关系,并以圆为背景来进行角度、长度和面积的计算 , 体现了试题考查数学素养的理念.
探究新图形的目的,是利用新图形来解决有关数学问题 , 实现从掌握基础知识、基本技能到自主建构、最终形成系统化知识的目的.
试题综合考查了学生应用基础知识和基本技能、数学思想与解题方法的能力,以及合情推理和演绎推理解决问题的能力.这是对学生基本数学素养的考查,也是该题的育人价值所在.
推荐阅读
- 核心|中科大陈秀雄团队成功证明凯勒几何两大核心猜想,研究登上《美国数学会杂志》
- 载体|可储氢的“纳米巧克力”结构创建
- 地铁|信号女子突击队:巧手“绣”出铁路“神经网”
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 半月|男子苹果官网订购iPhone 13 Pro Max:半月后却收两包巧克力
- 数学|中考数学阴影部分面积计算方法总结
- 人物|男子苹果官网订购iPhone 13 Pro Max:半月后却收两包巧克力
- 简写|Win10/Win11学院:Windows 本地搜索技巧总结
- wx|微信小技巧:只要用过网页版文件传输助手你就可以使用网页版微信
- 种业|哈尔滨市农业科学院联手校企建构智慧农业







