物理|杨-米尔斯规范原理和粒子物理标准模型丨庆贺杨振宁先生百岁华诞( 四 )_标准模型|科学|原子核|科普|科

在经典电磁理论中，这两种观点似乎各有千秋。从概念体系的简单性来看，似乎第一种观点还多点好处。但是量子力学出来以后就不同了。在量子理论中，电子的波函数ψ(x)可取复数值，其中x是时空点的坐标。因为只有波函数模的平方代表几率密度，我们可以对电子波函数做以下的位相变换：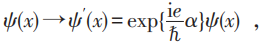

其中e是电荷， ?是普朗克常数， α 是个实的角度参数 (0≤α<2π) 。在没有任何相互作用的情况下，这是自由电子的一个对称性变换，它保持系统的作用量不变，从而导致电荷守恒定律。数学上，当参数α跑遍所有可能的值，这些变换形成一个群，叫做U (1)群。在量子场论中，每一个时空点上有一个希尔伯特空间，上式中的参数α应该换为时空点的任意实值函数f (x )：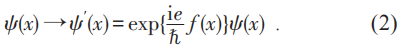

这样的以时空函数作为参数的变换，就是电子场(或波函数)的(局域)规范变换。
按照定域相互作用原理，电子场有电磁相互作用的理论也应当在电子场的规范变换(2)下不变。但是因为场的时空偏导数不满足和场同样的变换，多出了一个附加项：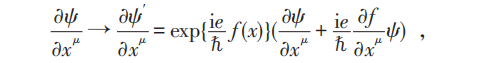

因而作用量或运动方程中有含电子场的(时空) 偏导数因子的项，在规范变换(2)下就不再是不变的 (或协变的) 。这个问题可以通过以下的办法来解决：第一步，引入一个新的规范势Aμ(x)以定义协变偏导数算子，即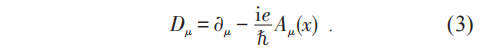

第二步，处处用协变导数Dμ替代普通导数?μ ，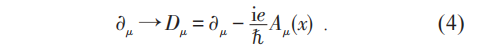

第三步，要求规范势的规范变换规则就是麦克斯韦理论中的规范变换(1) ，这就保证了电子场的协变导数在电子场规范变换(2)下是协变的，亦即协变导数像场一样变换：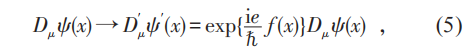

这里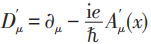

。第二步的规则(4)就是量子力学中引入电子与电磁势耦合(即相互作用)的“最小耦合替代规则” 。
由此可见，经典的麦克斯韦理论中电磁势的规范变换和规范不变性其实来源于量子理论，即电子 (或任何带电粒子) 的波函数或者场的(局域)位相变换不变性！后者又是与量子理论中的电荷守恒定律密切相关的深刻的对称性！杨先生就是抓住了麦克斯韦理论是一个规范场理论的实质，要在对称性和规范场理论的水平上推广麦克斯韦理论。

物理|杨-米尔斯规范原理和粒子物理标准模型丨庆贺杨振宁先生百岁华诞( 四 )

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)