这里我们必须提及二十世纪一位在物理学和数学领域享有盛誉的德国女物理学家及数学家——艾米·诺特(Emmy Noether , 1882-1935) , 她提出的 诺特定理 揭示了物理系统对称性与守恒量之间的深刻联系 , 其在现代物理学中出于核心地位 。
本文图片
图三:艾米·诺特 。 图片来自网络
诺特定理说的就是 , 在一个物理系统中 , 如果发现该系统具有某种对称性 , 那么一定存在一种与之对应的物理量 , 这个物理量在该系统中是一个守恒量 。 也就是说物理系统的对称性与守恒量是一一对应的 。
也许一些读者看到这里依然会感到茫然 , 因此我们尝试用一些简单的例子去理解诺特定理 。 我们在上中学的时候就学过能量守恒定律和动量守恒定律 , 知道在宇宙中能量和动量都是守恒量 。 诺特女士发现 , 这些守恒量都对应某一种对称性(symmetry) , 就是在物理系统具有某种与之对应的对称关系 。
那么如何简单地理解物理系统的“对称性”呢?举例来说 , 我们生活的宇宙就是一个完整的物理系统 , 这个物理系统中所有的物理定律都不会因为时间的改变而发生变化 , 比如说牛顿时代发现的牛顿定律与我们今天看到的牛顿定律在形式上都是一样的 , 这种关系就是对称性 , 或者不变性(invariance) 。 我们生活在的这个物理系统具有“时间对称性” , 根据诺特定理 , 这种“时间对称性”一定对应系统中的一种守恒量 , 这个守恒量被发现就是能量 。 于是 , 能量守恒定律就有了更加深刻的物理思想 , 它是一种系统的对称性的体现 。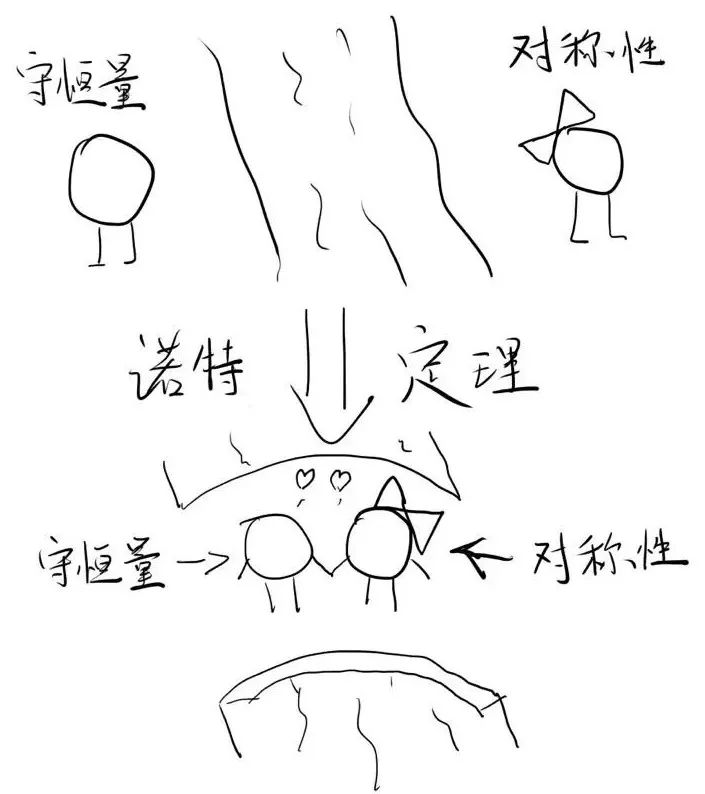
本文图片
图四:诺特定理如同鹊桥一样 , 让天各一方的两个角色 , 守恒量(牛郎)和对称性(织女)合二为一
另一个例子是 , 宇宙中的物理定律是放之四海而皆准的 。 比如牛顿第二定律的形式不论是在地球上还是在月亮上都是一样的——物理定律的表达不会因为空间位置的改变而发生变化 , 这种关系也是一种“对称性” , 从而我们可以得出结论 , “物理定律关于空间位置是对称的” 。 根据诺特定律 , 它也一定对应一种系统中的守恒量 , 这种守恒量被发现就是动量 。 能量守恒和时间对称 , 动量守恒和空间对称之间的亲密关系都可以通过数学严密地计算出来(小编注:可参考文献 [5] 的第 20 章) 。
笔者注:物理系统中所有的物理定律都由数学方程来表达 , 例如牛顿力学有牛顿第二定律 , 电磁学有麦克斯韦方程等等 , 这些数学方程都有自变量 , 比如时间变量或者空间变量 。 对于对称性更严格的表述是 , 当这些自变量发生某种变换的时候(例如空间位置的平移 , 时间的平移) , 刻画这个系统的方程形式保持不变(方程的协变性) , 那么我们就说这个物理系统在这种变换下具有对称性 。 诺特定理就是说 , 系统的一种对称性一定对应于系统中的一种守恒量 , 在这个例子中 , 时间的平移对称性就对应于系统的能量守恒 , 空间的平移对称性就对应于系统的动量守恒 。 诺特定理在数学上得到了严格的证明 。 虽然数学家们对它并不太重视 , 但对于物理学来说 , 它具有更加深刻和重要的意义和极大的启发性 。 通过诺特定理我们知道了 , 我们在物理学中所研究的种种守恒的物理量 , 其本质上都是物理系统自身所具有的某种对称性的一种体现 。 反过来思考 , 如果我们能够发现物理系统的一种新的对称性 , 那么通过诺特定理 , 我们就能够找到系统的一种新的守恒的物理量 。 也是因为这个原因 , 诺特成为了现代理论物理学的鼻祖之一 。
推荐阅读
- 历史|科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 空间|(科技)科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 平板|消息称 vivo 平板明年上半年推出:骁龙 870,四边等宽全面屏设计
- 硬件|汽车之家年底裁员,员工称多个职能部门已被撤销
- ASUS|华硕预热ROG Flow Z13:称其是“全球最强悍的游戏平板”
- 视点·观察|科技巨头纷纷发力元宇宙:这是否是所有人的未来?
- Monarch|消息称微软Win11 2022重大更新将在明年夏天到来
- Apple|法官称苹果零售店搜包和解协议虽不完美,但可继续进行
- IT|报道称Polestar 4电动SUV将跟保时捷Macan电动版对标
- 虚拟|比尔·盖茨关于2022年的五项预言之二:元宇宙成有用的工具







