

等角线是空间中相交于同一个点的一组直线 , 而这些直线中两两形成的夹角都相等 。
在二维平面中 , 正六边形的三条对角线就是一组等角线 , 任意两条线形成的夹角都是60° 。 同时 , 这种情况也是二维中等角线数量的极限 , 换句话说 , 在二维中等角线最多有三条 。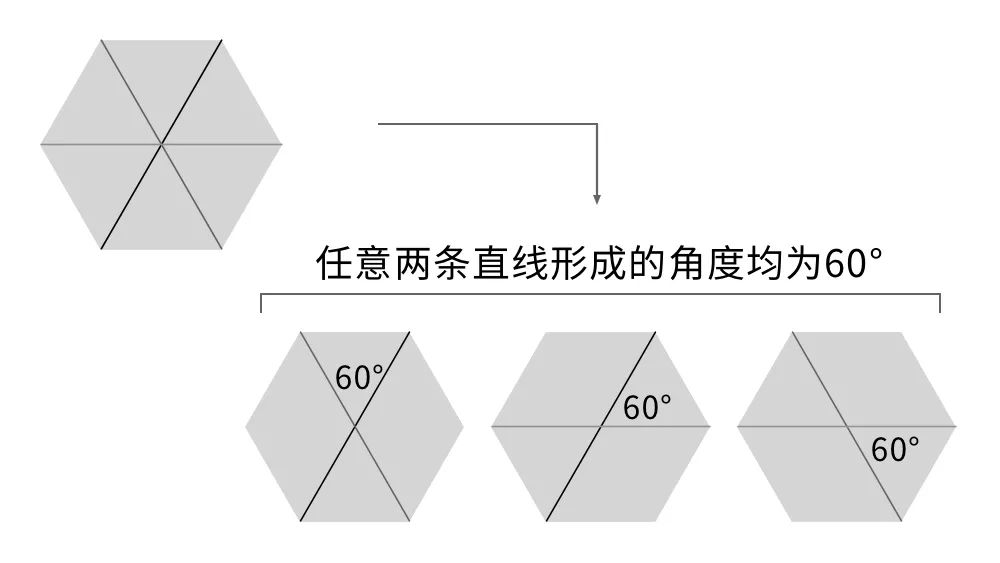
二维平面中的等角线 。 | 图片来源:毛尖尖;素材参考:Lucy Reading-Ikkanda/Quanta Magazine
而在三维空间中 , 连接正二十面体相对顶点的6条线同样是一组等角线 , 它们两两之间会形成63.4°的夹角 。 这组等角线数量也是三维空间中的最大值 。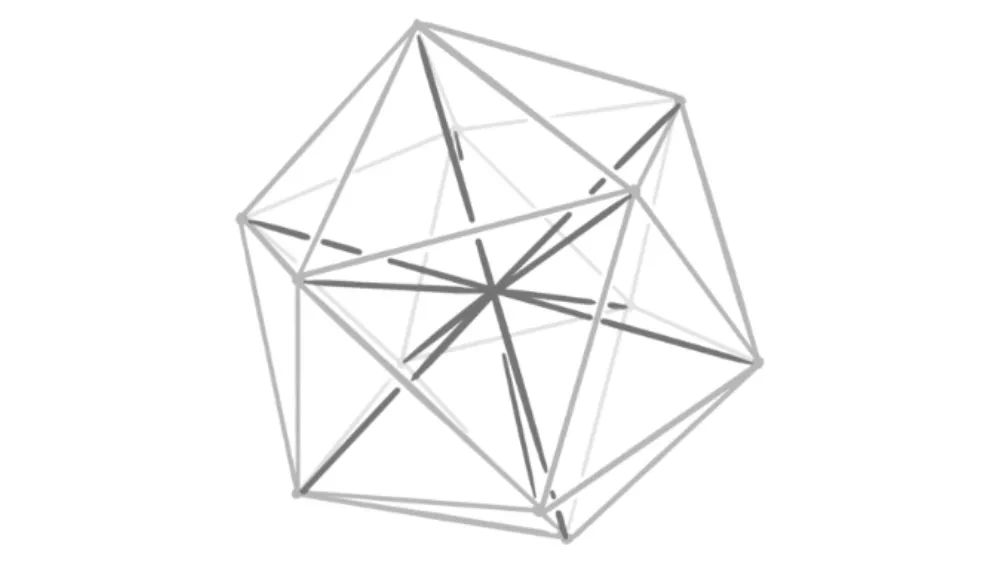
三维空间中正二十面体和6条等角线 。 |图片来源:Zilin Jiang / MIT
但对数学家来说 , 探索并不局限于三维空间 。 在一些数学家眼中 , 高维才真正让事情开始变得有趣 , 其中似乎包含着无限可能 。
但对等角线而言 , 它们在高维中并不是无限的 。 麻省理工学院的赵宇飞和他的团队尝试解决了高维空间中这个直线几何的问题 。 这个问题困扰了研究人员至少70年 。 这项突破确定了高维中给定角度的等角线的最大可能数量 。 论文即将发表在2022年1月的《数学年刊》上 。
当维度超过三时 , 我们不可能真正在脑海中想象得出等角线的构造是什么样子的 , 这也是为什么计算任何维度中等角线的最大数量是非常困难的 。
自上世纪中叶起 , 等角线的极值几何研究已经开始受到广泛的关注 。 1973年 , 数学家莱门斯(P. W. H. Lemmens)和塞德尔(J. J. Seidel)在一篇发表于《代数学报》的论文中详细阐述了研究给定角度的等角线的最大数量的问题 。
但之后的几十年 , 对相关问题的研究停滞了很长一段时间 。 直到几年前 , 2017年 , 数学家苏达科夫(Benny Sudakov)带领的研究团队在等角线最大数量的研究中取得了一些重要进展 。
从本质上来说 , 苏达科夫沿用了研究“不可观察”的对象时经常使用到的数学方法 。 他们寻找其他类型的数学对象来表示直线的存在 。 简单来说 , 他们将这些直线和向量及其运算联系在了一起 , 并将其转化成矩阵 。 这样一来 , 线性代数的工具就顺理成章地被引入 , 从而进行进一步探索 。
推荐阅读
- 核心|中科大陈秀雄团队成功证明凯勒几何两大核心猜想,研究登上《美国数学会杂志》
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 数学|中考数学阴影部分面积计算方法总结
- 处理|我们计划招收300名数学爱好者,免费系统学习Matlab与傅立叶变换
- 问题|第六届“复旦-中植科学奖”授予两位数学家
- |数学家就是那些发现了数学之美的人
- 想象力|“天才数学家只有极少数,我肯定不是”
- 全球|2021复旦科技创新论坛在沪举行 两数学家荣获第六届“复旦-中植科学奖”
- Massive|华为联合中科院数学与系统科学研究院成立“π 实验室”
- 影响|为数学而疯的大数学家(转)







