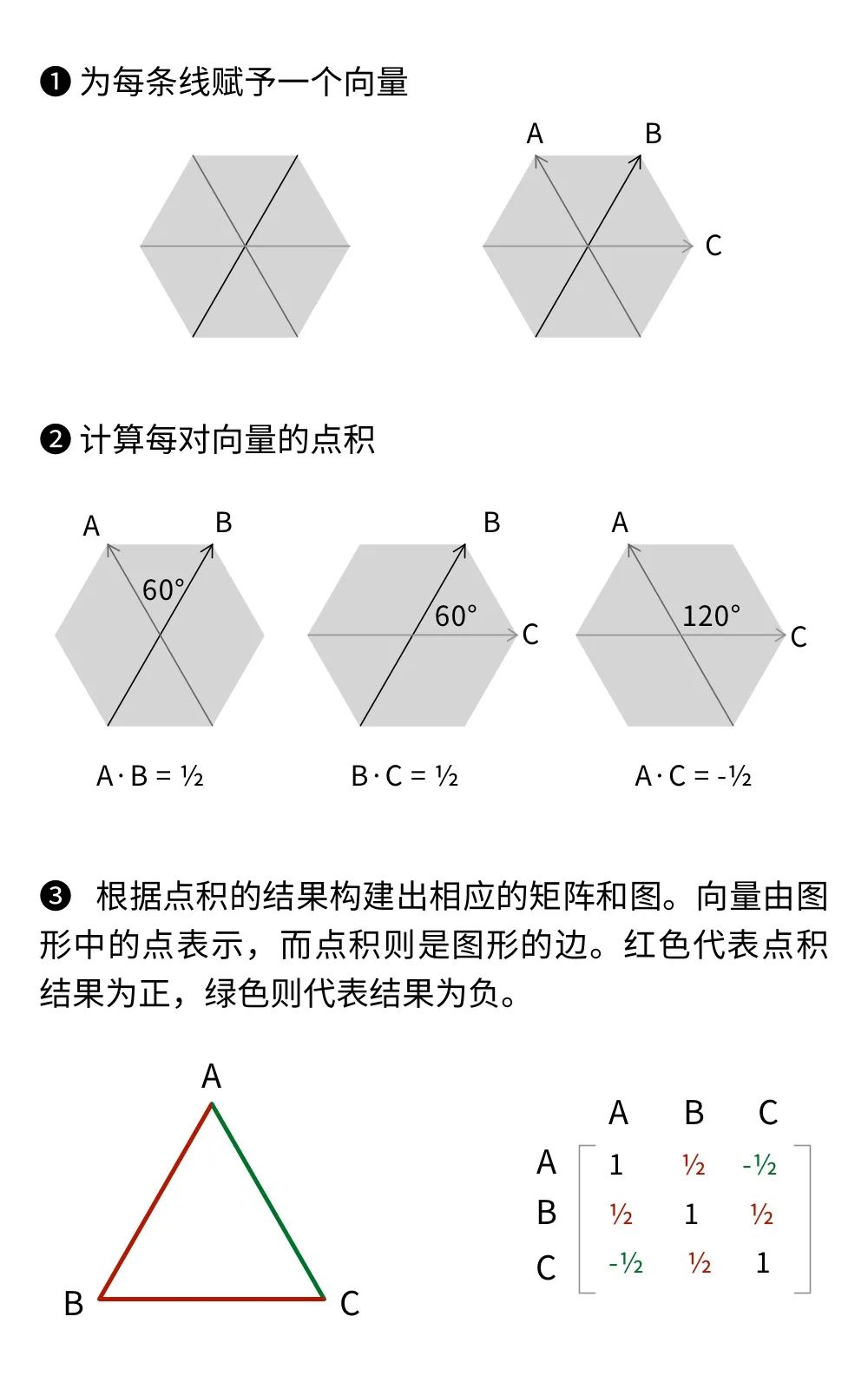
苏达科夫使用到的方法在二维中的简化版示意 。 |图片来源:毛尖尖;素材参考:Lucy Reading-Ikkanda/Quanta Magazine
图论是一种研究点如何通过边相互连接的学科 。 借助图论的语言重新解构并分析这个几何问题后 , 研究的主要创新便随之显现 。
在这个等角线问题中 , 图形的点就表示向量 。 点根据特定的颜色规则相互连接 , 将红色和绿色的线进行配置 , 从而构建出了一种截然不同的方式来审视原来那个问题 。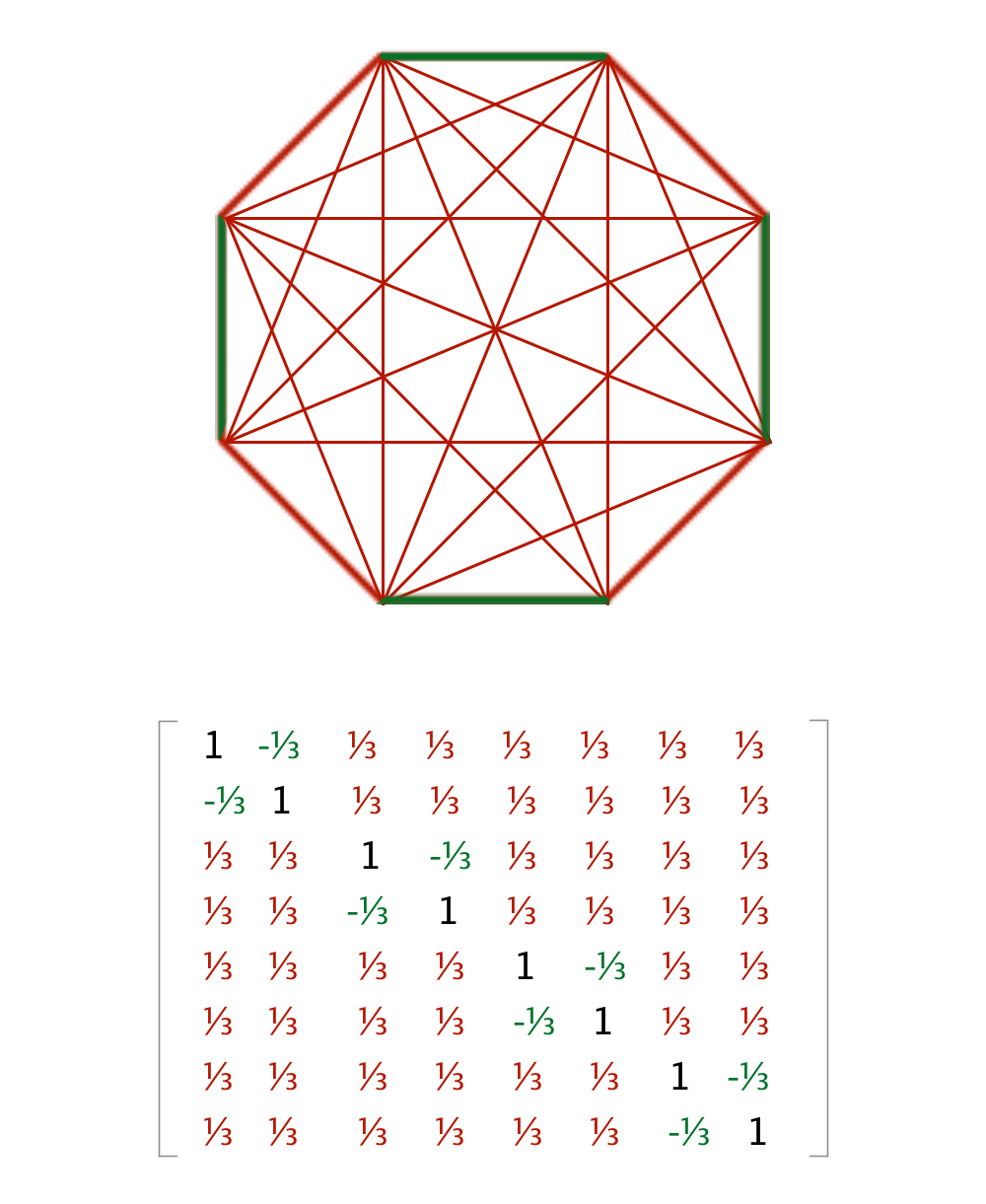
类似的方法也可以应用在更高维度中 , 比如五维中8条直线的图和矩阵 。 |图片来源:毛尖尖;素材参考:Lucy Reading-Ikkanda/Quanta Magazine
在苏达科夫取得这项进展后不久 , 他前往MIT进行访问活动 , 并在组合学研究研讨会上谈到了他在等角线方面的进展 。
赵宇飞在采访中表示 , 着手研究这个问题是因为他原本正在寻暑期项目课题 , 他认为等角线是一个有待解决的大问题 , 也相信团队可能会取得一些不错的进展 。 但最终完全解决整个问题绝对超出了他的预期 。
在这项新研究中 , 团队仍然是借助线性代数的工具去理解图和网络 , 通过图形及其转化后的矩阵来得到所谓的“谱” , 也就是所谓谱图论的方法 。 用赵宇飞的比喻 , 这就好比用一束强光照在一张图上 , 然后检查出现的颜色光谱 。
团队在这些谱中发现了一些之前从未被观察到的基本事实 。 新的研究带来了谱图论中的一个新定理:有界度图必须具有次线性第二本征值重数 。 这个定理的证明需要格外的洞察力 , 将图的谱与图中小块的谱联系在一起 。 而他们的证明清晰而明了 。
这篇论文为谱图论领域提供了新的见解 , 并为研究网络提供了数学工具 。 谱图论已经引出了计算机科学中的不少重要算法 , 如谷歌搜索引擎的PageRank算法 。
这种对等角线的新理解同样对编码和通信具有潜在的重要意义 。 等角线是“球形码”(spherical code)的一个例子 , 这正是信息论中的重要工具 , 它允许各方通过嘈杂的通信信道互相发送信息 , 比如NASA与其火星探测器之间的通信 。
#创作团队:
编译:M?ka
#参考来源:
https://news.mit.edu/2021/mathematicians-solve-old-geometry-problem-equiangular-lines-1004
https://www.quantamagazine.org/a-new-path-to-equal-angle-lines-20170411/
#图片来源:
封面来源:Zilin Jiang / MIT;封底:Pixabay
推荐阅读
- 核心|中科大陈秀雄团队成功证明凯勒几何两大核心猜想,研究登上《美国数学会杂志》
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 数学|中考数学阴影部分面积计算方法总结
- 处理|我们计划招收300名数学爱好者,免费系统学习Matlab与傅立叶变换
- 问题|第六届“复旦-中植科学奖”授予两位数学家
- |数学家就是那些发现了数学之美的人
- 想象力|“天才数学家只有极少数,我肯定不是”
- 全球|2021复旦科技创新论坛在沪举行 两数学家荣获第六届“复旦-中植科学奖”
- Massive|华为联合中科院数学与系统科学研究院成立“π 实验室”
- 影响|为数学而疯的大数学家(转)







