文章图片
在 [0, β] 中被支持 , 则 N = RQ 是一个可被所有小于 βQ 的素数整除的无平方整数 , 可得到以下方程:
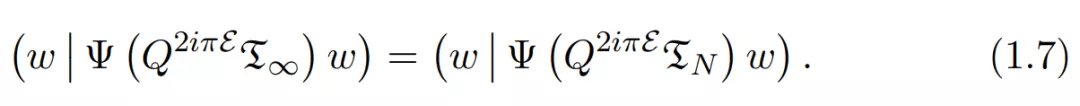
文章图片
现在 , 右侧的厄米特形式适用于代数算术版本 。 实际上 , 将 half-line 支持的
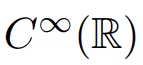
文章图片
中的函数传递到以下方程定义的线性情况下
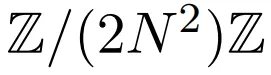
文章图片
上的函数:
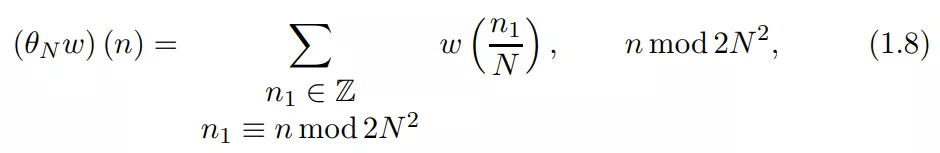
文章图片
与 [1] 中已获得的证明结果相比 , 新研究在于充分利用了这种代数结构和测试函数 w 的支持假设 。 作者通过进一步的条件
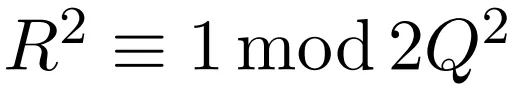
文章图片
来利用一切可能性约束 R , 然后主厄米特形式(1.7) 本质上等于 Q^2 乘以「简化」形式
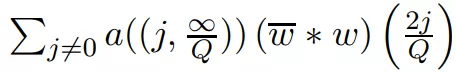
文章图片
。 如果假设 w 在 [0, β] 中得到支持 , 对于某些 β , 则可以使用主厄米特的简单无条件估计形式 , 也就能够对简化形式实现非常好的估计 。 为了从中推导出黎曼猜想 , 剩下要做的是为简化形式提供一个类似于(1.5)的标准 。
是民科?还是正经研究?有待同行评议
对于 André Unterberger 这篇证明黎曼猜想的论文 , 有知乎用户吐槽称 , 「有点像 mathgen(一种数学论文生成器)自动生成的 。 」
文章图片
不过 , 更多的网友还是给予了肯定与期待 。 有位匿名用户认为 , 「作者毕竟是法国数学家 & 1950 年菲尔兹奖得主 Laurent Schwartz 的博士生 , 法国数学家 & 1966 年菲尔兹奖得主 Alexander Grothendieck 的同门师弟 , 年逾 80 , 总归非民科能碰瓷的吧 。 」
文章图片
这位匿名用户的观点也得到了其他人的附议 。 「至少看上去有可能是对的 , 比某精细结构常数要靠谱得多 。 仍有很大可能存在缺陷 , 还是期待同行评议的结果 。 」有用户这样表示 。
文章图片
总之 , 对于这篇「不明觉厉」的文章 , 挂在了 arXiv 数论板块(Number Theory)也在一定程度上说明了作者并非胡说臆测 。 如果有读者大神研究这一证明 , 欢迎留言告诉我们结果 。
推荐阅读
- 数字货币|币安在法国扩张业务 项目规模1亿欧元
- Siamese|一个框架统一Siamese自监督学习,清华、商汤提出简洁、有效梯度形式,
- IT|美国法国英国连创历史新高 世卫组织警告“感染海啸”到来
- 法国|奥密克戎对抗体存大量逃逸现象
- 研讨会|国内外专家学者共议智慧城市发展趋势
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 形式|“摇一摇”就进广告页面?这些APP承诺整改
- 频段|我学者提出拍赫兹通信新框架 助力未来6G发展
- 通信技术|我学者提出拍赫兹通信新框架 助力未来6G发展
- 墨水|美媒揭秘:法国王后玛丽·安托瓦妮特的密信







