原创 Philip Ball 返朴
自然界中有不少神奇现象令人震撼 , 你能想到蜂巢、肥皂泡和海绵外骨骼之间的奇妙联系吗?答案是它们钟爱六边形 。 为何蜜蜂会打造出完美的六边形蜂巢?这当然不是什么神秘的力量 , 而是其中富含的深刻数学和物理学道理 。
撰文 | Philip Ball
编译 | 顾淼飞
蜜蜂 , 天生的数学家?
蜂巢简直是个工程学奇迹:它由一排排棱镜似的“小隔间”组成 , 每一个“小隔间”的横截面都是完美的六边形;由蜂蜡制成的墙壁 , 每一面的厚度都相当精确;所有的房间沿水平方向微微倾斜 , 不仅避免蜂蜜从蜂巢里流出来 , 还让整个蜂巢的方向与地球磁场方向一致 。
蜜蜂在动工之前并没有做过统筹规划 , 也不可能拿到设计图纸 , 它们却能分工合作 , 鬼使神差地完成了如此精妙绝伦的蜂巢 。
蜜蜂是怎么做到的?
古希腊哲学家帕普斯(Pappus of Alexandria)认为 , 蜜蜂一定天赋异禀 , 有着“几何学的远见卓识” 。 那么 , 又是谁给了它们这种远见卓识 , 似乎只能是上帝吧?莫非蜜蜂果真像威廉·柯比(William Kirby)在1852年说的那样 , 是“天生的数学家”?不管你信不信 , 反正达尔文不信 。 达尔文认为主导这一切的是进化论 , 而不是什么神祗的力量 , 于是他进行了一系列实验 , 想证实蜜蜂是否仅凭进化和遗传得来的本能就可以建造出完美的蜂巢 。
下一个问题是 , 为什么是六边形?这其实是一个很简单的几何问题 。 假设我们想用相同形状和大小的图形密铺一个平面(使图形不留空隙、也不互相重叠地铺满整个平面) , 那么只有3种正多边形可以做到:正三角形、正方形和正六边形 。 (这里指规则镶嵌 。 关于不规则镶嵌可参见《》 。 )在铺满同等面积的情况下 , 使用正六边形所需要的周长之和最小 。 这就不难理解蜜蜂为什么会选择六边形了 , 因为蜂巢是用蜂蜡做的 , 而蜜蜂产出蜂蜡是消耗能量的 , 它们当然希望省些力气——这点小心思就跟打工人想少搬几块砖一样 。
人们早在18世纪就明白了这一点 , 用达尔文的话说 , 六边形的蜂巢是“最省劳动力、也最省材料的选择” 。 他认为 , 既然六边形蜂巢所需要的能量和时间是最少的 , 那么在自然选择的作用下 , 这种建造方式就成了蜜蜂的本能 。 不过 , 就算蜜蜂真的会测量巢房的角度 , 会测量墙壁的厚度 , 它们也未必需要依赖这种本能 。 因为 , 创造六边形是大自然一贯的做法 。
大自然更爱“斤斤计较”
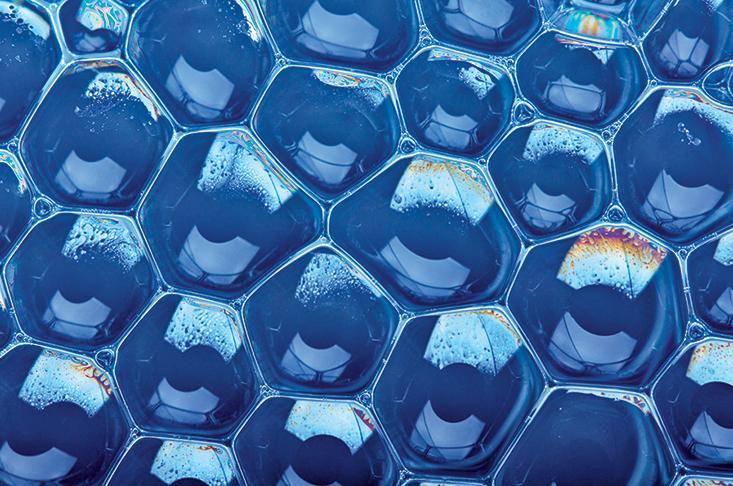
如果你在水面上吹一层泡泡——也就是“泡泡筏(Bubble raft)”——这些泡泡最后都会变成六边形或者近似于六边形的形状 。 你不可能看到有哪个泡泡筏里全是正方形的泡泡 , 如果有4个泡泡聚集在了一起 , 它们会马上重新排列成“三足鼎立”的样子 , 交界处就像经典的奔驰标志 , 三边相接 , 夹角差不多都是120° 。
文章图片
单层的“泡泡筏”由大多数六边形(不一定是正六边形)的泡泡组成 。 有一些“缺陷”泡泡可能有五面或七面 。 但三边相交 , 角度约为120° 。 图源:Shebeko / Shutterstock
蜂巢中的六边形尚且有个“幕后推手”——说的就是蜜蜂 , 而泡泡筏中的六边形可并没有什么神秘力量在驱使 。 如果硬要说有 , 那么这个神秘力量就是物理学规则 。 (参见《》)
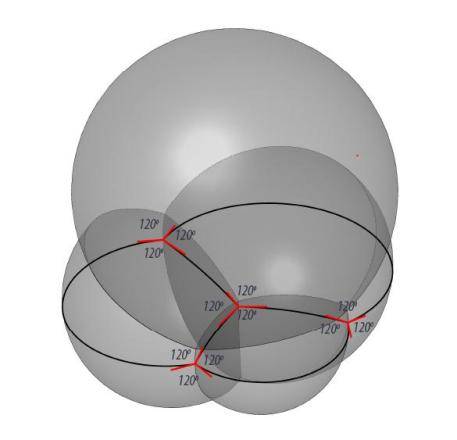
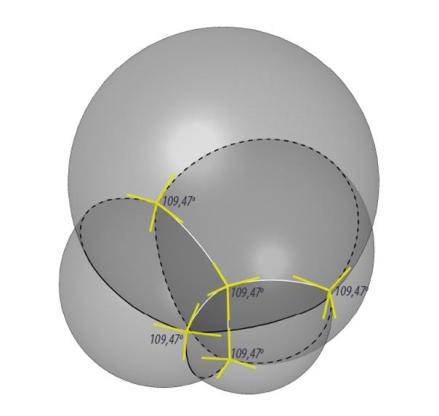
如果我们从平面的泡泡筏推演到立体的“泡泡堆” , 结果也是类似的 。 假如你用吸管对着一碗肥皂水吹气 , 吹起一堆泡沫 , 你会看到 , 当泡泡堆积在一起之后 , 它们四面边界相交于一个点 , 夹角约为109°——没错 , 这个角度就是正四面体中心到各顶点连线的夹角 。
文章图片
文章图片
根据普拉托定律 , 肥皂泡表面的交界一定是由三个表面相交构成的曲线 , 被称为普拉托边界 , 它们的交角为120° 。 普拉托边界之间相交一定是由四条边界相交构成一个点 , 两两边界交角为109° 。 丨图源:wewanttolearn.wordpress.com
泡泡筏和泡泡堆中的连接方式是由谁决定的呢?大自然显然比蜜蜂更会算账 。 泡泡和皂膜是由水组成的(当然 , 表面有一层皂液分子) , 作用于液体表面的表面张力会拉动泡泡 , 让其表面积尽可能的小 。 这就是为什么雨滴大致呈球形的原因 , 因为在相同体积下 , 球形的表面积是最小的;水滴在蜡质叶片上会缩成水珠 , 也是同样的道理 。

文章图片
当水洒在疏水表面时 , 它可能会分裂成水滴 。 液滴的形状最终由表面张力、重力和作用于水和水与固体表面之间的力决定 。 表面张力将液滴拉成大致的球形 。 如果后两者更强 , 水滴就会像透镜样平铺在表面上 。 如果疏水性不强 , 小水滴就会扩散成一层平坦光滑的薄膜 。 丨图源:Stuchelova, Kuttelvaserov/Shutterstock;Olgysha/Shutterstock;Pitiya Phinjongsakundit/Shutterstock
现在我们知道了表面张力决定泡泡的连接方式 , 泡沫总会找到一种具有最小表面张力的结构 , 也就是使总表面积最小的结构 。 但是 , 关于泡沫的结构还需要考虑另一个问题 , 即力学上的稳定 。 在连接点处 , 沿着不同方向的作用力必须达到平衡 。 无论是泡泡筏的平铺还是泡泡堆的四面相连 , 都是能满足这一要求的连接方式 。
有人认为 , 蜂巢也可以看作是蜂蜡凝固之后形成的“泡泡筏” , 但这就无法解释为什么造纸胡蜂(paper wasp , Polistes dominula)的蜂巢里也是六边形组成 。 它们的窝可不是蜂蜡做的 , 而是它们自己的唾液与木材纤维、茎等混合咀嚼之后得到的糊状“纸浆” 。 表面张力在其中起不到什么作用 。 而且 , 不同类型的黄蜂遗传了不同的建筑设计能力 , 这种差别很明显 。

文章图片
用自己分泌的柔软蜂蜡搭建完美六边形蜂巢 , 蜜蜂似乎是进化出了这种能力 。 但也有些研究者认为 , 柔软的蜂蜡上本身存在的表面张力就足以把每个“小隔间”拉伸成特定的形状 , 就像泡泡筏中的泡泡堆积一样 。 丨图源:Grafissimo / Getty
力学规律只告诉了我们泡泡之间的连接方式 , 却没有告诉我们泡沫里的每一个泡泡最终会形成什么形状 。 仔细看 , 这些泡泡是具有不同形状和大小的多面体 , 多面体的边都不是笔直的直线 , 多少带有一点点弧度;有的面有五条边 , 有的面有六条边 , 也有的只有四条甚至三条边 。 这是因为泡泡内的气体压力与气泡体积成反比 , 大气泡旁边的小气泡会向外膨胀 , 发生轻微的弯曲 , 所以这些不同形状的多面体都能通过适当的微调 , 形成四面相接的稳定结构 。 尽管它们遵守一些几何规则 , 但也相当混乱 。
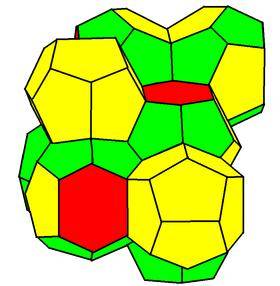
有没有那种所有泡泡都是一样大小的“完美”泡沫堆呢?什么样子的泡沫堆既能使得泡泡的表面积总和最小 , 又能在连接处满足角度的要求呢?这个问题已经争论了很多年 。 在很长一段时间内 , 人们认为理想的泡泡形状是由6个正方形和8个正六边形表面围成的十四面体(截角八面体) 。 直到1993年 , 都柏林三一学院的两位物理学家Denis Weaire和Robert Phelan发现了一种不那么规则、表面积却更小的结构 , 它由8种不同形状的泡泡重复排列而成 。 后来 , 这个略显复杂的图案出现在了2008年北京奥运会游泳馆“水立方”的外立面上——它就是“水立方”泡沫图案的设计灵感来源 。
文章图片
Weaire-Phelan的泡沫结构丨图源:wiki
生物细胞中出现的一些图形 , 也遵循了泡泡结构的形成机制 。 例如 , 苍蝇的复眼是由一个个六边形组合在一起的 , 就像泡泡筏中那样;每一只小眼的感光细胞 , 也是四个四个地连接在一起 , 就像泡泡堆一样 。 即使在发生了突变的苍蝇身上 , 它们眼睛里每一组感光细胞不止四个 , 其排列方式仍然跟泡泡模式大致相同 。
【蜂巢|自然界为何处处是六边形?这里有深刻的数学和物理】
文章图片

文章图片
气泡和泡沫在自然界中也有实际用途 。 图中展示的是一种浮挂在海中生活的紫蜗牛 , 泡泡包裹着它们分泌的粘液形成浮筏使 , 它们以捕食生活在水面的小生物为生 。 丨图源:Dorling Kindersley;Denis Riek
表面张力塑造极小曲面
同样由于表面张力 , 皂膜会沿着闭合的线框形成一个平整的薄膜——想想看 , 你在吹泡泡时 , 塑料圈上是不是出现了一层膜?如果线框被弯折 , 那么皂膜的表面也会跟着弯曲 。 皂膜最终成型的曲面 , 就是能覆盖整个空间 , 并且是表面积最小的一种形状 。 如果你是一名建筑师 , 你就可以从中学到怎样用最省材料的方式建造屋顶 。 事实上 , 很多建筑师比如如弗雷·奥托(Frei Otto)确实会从皂膜那儿“偷师学艺” , 他们青睐“极小曲面”在几何造型上的美丽与优雅 , 当然也因为这样做更省耗材 。

文章图片
德国建筑师、工程师弗雷·奥托致力于使用最少的材料进行设计 , 创造了众多经典建筑 。 图为建于1963年德国汉堡的国际园艺展馆 。 图源:Atelier Frei Otto Warmbronn
所谓“极小曲面” , 是指平均曲率为零的曲面 。 在表面张力的作用下 , 每一个表面都在“追求”最小 , 不仅要让表面积最小 , 也要让平均曲率趋于最小 。 曲率 , 是表征弯曲程度的概念 , 弯曲得越剧烈 , 曲率就越大 。 曲率可以是正值(外凸) , 也可以是负值(内凹 , 或者说鞍形) 。 因此 , 只要正负曲率互相抵消 , 这个曲面的平均曲率就为零 , 从而成为一个极小曲面 。
如果一个极小曲面可以把空间分隔成由各式通道按照一定规律组成的网络系统 , 那么这个曲面就叫作周期性极小曲面 。 (这里的周期性是指一组结构不断地重复出现 , 或者说整个图形是有规律的 。 )这样的曲面在19世纪被发现时 , 似乎只被当成了数学家捣鼓出来的玩具 , 但是现在我们知道 , 这是自然界用表面张力创造出来的绝妙规律 。 (值得注意的是 , 数学上证明极小曲面和物理上的构造并不等同 。 )
当极小曲面出现在生物的细胞或外壳
从植物到鱼类再到大鼠 , 它们的细胞中都能找到这种具有极小曲面的膜结构 。 至于这种膜结构的确切作用 , 也许是用来隔开不同的生化反应 , 避免相互影响;也许是为了用最少的材料创建最多的“工作表面” , 之所以这么说 , 是因为膜表面分布有大量的酶或其他活性分子 , 能进行多种生化反应 。 暂且不管它的功能是什么 , 创造这种结构其实并不需要一套复杂的“基因说明书” , 物理学规则自会搞定这一切 。
有些种类的蝴蝶 , 例如欧洲的黄星绿小灰蝶(green hairstreak , Callophrys rubi)和宽绒番凤蝶(emerald-patched cattleheart , Parides sesostris) , 其翅膀鳞片上就有一种周期性极小曲面——螺旋二十四面体(gyroid) 。 从曲面的凸起处和从其他结构处反射回来的光波之间会发生干涉 , 波长的变化也就意味着颜色的消失或出现 。 这就是翅膀鳞片产生颜色的特别技巧 。

文章图片

文章图片
黄星绿小灰蝶(Callophrys rubi)翅鳞的微观结构 。 D图为模拟的螺旋二十四面体结构 。 丨图源:butterfly-conservation.org;PANS , doi.org/10.1073/pnas.1511354112
头帕科的一种海胆(Cidaris rugosa)的外骨骼也包含多孔网状的结构 , 这是另一种周期性极小曲面 。 外骨骼会长出长长的尖刺 , 主要成分跟白垩和大理石一样 , 都是碳酸钙 。 而这种多孔网状的结构让外骨骼既坚固又轻便 , 有点像制造飞机时使用的泡沫金属 。

文章图片

文章图片
Cidaris rugosa丨图源:wiki;Christopher Mah/echinoblog
海胆是怎么用碳酸钙这种坚硬、不易变形的矿物做成多孔网格的呢?显然 , 它们应该先是用柔软灵活的膜制作了一个内部互通的网状模具 , 然后再让坚硬的材料在模具内部结晶成型 , 成为类似于泡沫金属的“泡沫矿物” 。

文章图片
阿式偕老同穴海绵(Euplectella aspergillum英文俗称维纳斯花篮)的多孔骨架 , 就像凝固的泡沫构成——矿物质就填充在泡状软组织的交界处周围 。 图源: Dmitry Grigoriev / Shutterstock
这个办法还可以用来实现更复杂的目的 。 比如 , 光线在这种网状结构中会发生多次反射 , 形成复杂迂回的反射路径 , 这些泡沫矿物就像镜子 , 可以用来控制或引导光线的传播方向 。 鳞沙蚕(Aphrodita aculeata , 一种海洋多毛类蠕虫)就是这样做的 , 它们的几丁质外棘刺内含有中空的蜂巢式微管 , 这些看似像毛发的结构就成了天然可引导光线的光纤 。 它们可以根据光照方向改变身体颜色 , 这似乎就是它们震慑捕食者的手段 。

文章图片
鳞沙蚕因其体型和行动像老鼠 , 因此俗称为“海鼠(sea mouse)” 丨图源:wiki
海胆和鳞沙蚕等先用软组织或膜制作模具 , 再通过“浇铸”过程在模具内部形成具有特定形状的外骨骼的方法 , 即所谓的“生物矿化作用(Biomineralization)” , 在海洋生物中屡见不鲜 。 例如 , 一些海绵动物的外骨骼看上去像是脚手架 , 那其实就是条状矿物用这种方式连接起来的 , 而且 , 矿物“条”的连接处跟泡泡堆非常类似——如果表面张力塑造了这些结构 , 那就绝对不是巧合 。
生物矿化作用在放射虫和硅藻等海洋生物身上产生了无比瑰丽的视觉效果 。 一些放射虫和硅藻的外骨骼拥有精妙无比的图案:矿物组成了一个个六边形和五边形 , 而且排列得齐齐整整 , 你甚至可以管它们叫海中蜂巢 。 19世纪末 , 当德国生物学家(同时也是一名极具天赋的艺术家)恩斯特·黑克尔(Ernst Haeckel)第一次在显微镜下看到这些图案时 , 震撼的画面令他折服 。 惊叹之余 , 他将这些图案画了下来 , 并出版了绘画作品集《自然界的艺术形态》(Art Forms in Nature) 。 这部作品在20世纪初的艺术家之间非常有影响力 , 时至今日仍令人赞叹 。

文章图片
“不仅是图集 , 而是对世界观的总结” , 著名德国生物学史专家的Olaf Breidbach如此评价海克尔的作品 。 丨图源:Ernst Haeckel, Kunstformen der Natur (1904).
在黑克尔看来 , 生物身上展现出来的这些图案是大自然的神来之笔 , 可见大自然具有超乎想象的创造力和艺术表现力 。 当然 , 我们今天已经知道 , 这些图案真正的“幕后推手”不是什么神祗的力量 , 而是表面张力 , 尽管如此 , 我们依然不能否认他观念里的核心思想——
面对自然界创造出来的这些奇迹般的、无处不在的美丽 , 我们只有啧啧称奇的份儿 。
原文:http://nautil.us/issue/35/boundaries/why-nature-prefers-hexagons
版权说明:欢迎个人转发 , 任何形式的媒体或机构未经授权 , 不得转载和摘编 。 转载授权请在「返朴」微信公众号内联系后台 。
_原题《自然界为何处处是六边形?这里有深刻的数学和物理》
阅读原文
推荐阅读
- Windows|微软解释在Windows 11上为何部分驱动可追溯到1968年
- 体系|为何要推进智能制造?工信部:对实现新型工业化有重要作用
- 苹果|苹果配件必须买原装 这个错误言论为何误导了很多人?
- 销售额|全面进化的双芯2.0旗舰iQOO Neo5S,为何能成为“春节档”霸榜的大热门?
- 发射|耗资90亿美元,史上最强!詹姆斯·韦伯太空望远镜为何备受关注?
- 汽车|智己巡游为何要炫耀?
- 机器人|观察|自主移动机器人为何兴起,AGV、AMR趋势如何?
- 处理速度|OPPO为何要自研影像NPU芯片?采访OPPO芯片产品高级总监姜波先生
- 排名|为何一体化污水处理设备厂家排名有猫腻?
- 人物|为何力挺狗狗币而非比特币?马斯克这样解释







