大家一定都听过这样一个谚语:
一个和尚挑水吃
两个和尚抬水吃
三个和尚没水吃
这说明责任与分工真的很重要!
本文图片
如果磁铁也懂得这个道理的话
几个磁铁排列起来
是不是可以获得更强的磁力呢?
本文图片
实验器材
所标杯、绳子、透明塑料袋、小磁针、5个方形磁铁、长方体盒子、胶枪、钢珠
本文图片
实验过程
首先用小磁针判断磁铁的磁力方向
并在每一小块上做好标记
本文图片
用胶枪在长方体盒子上粘上一小段绳子
当做挂钩与塑料袋连接起来
本文图片
先试试第一种排列方式
本文图片
将排列好的磁铁条放入盒子内
本文图片
利用磁铁的磁性将装置固定在铁板上
本文图片
【海尔贝克阵列|1+1+1可以大于3吗? | 正经玩】慢慢的向塑料袋中放入钢珠
本文图片
发现第一种排列方式最多能放14个钢珠
?
本文图片
换一种排列方式
?
本文图片
本文图片
采取与上述相同的方法
发现可以放入的钢珠大大增加
?最多可以放112个!
本文图片
也可以试试这种排列的另一侧
本文图片
则只可以放9个钢珠
用下面这种排列方式时
本文图片
则可以放41个
原理解说
不同磁体以不同方式排列起来 , 各自的磁场经过叠加 , 其磁场强度的空间分布会有不同 。 这件事很容易理解 , 即使是单个磁体 , 其周围磁场的强度大小也不是均匀分布的 。
这次实验 , 我们把磁体按照不同的顺序纵向、横向交替排列 , 下面可以悬挂不同数目的钢珠 , 这说明小磁体上方的磁场强度是不同的 。 其中有一些排列顺序使得小磁铁某个方向的磁场强度得到了加强 。 这种特殊结构称为海尔贝克阵列 , 各个磁体的磁化方向按照阵列依次旋转某个角度 , 可以用最少量的磁体产生最强的磁场 。 周围的磁力线在小磁铁的上方聚集 , 达到最强;而下方的磁力线却非常稀疏 , 在空间中近似正弦分布 。
海尔贝克阵列
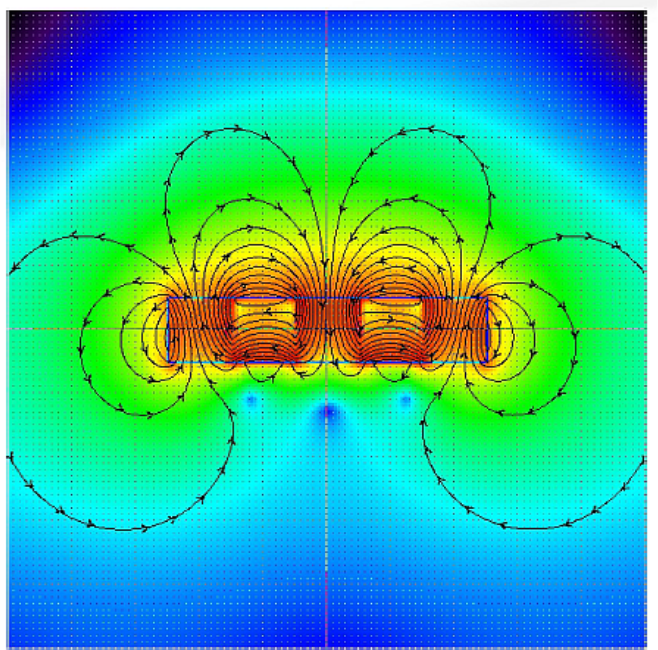
本文图片
海尔贝克阵列磁力线分布
(图源AZLoop Final Design Package)
海尔贝克阵列有不止一种 , 可以按照不同的需求设计不同的种类 。 将直线型海尔贝克阵列首尾相接 , 就可以得到环形海尔贝克阵列 。 制造海尔贝克阵列 , 可以像我们一样把小磁铁按照不同的排列顺序粘起来 , 也可以先把各个分段磁体粘起来 , 再一起充磁 。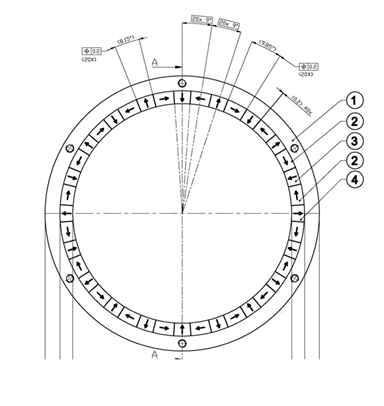
本文图片
环形海尔贝克阵列
海尔贝克阵列可以加强单边磁场 , 在生活中有着广泛的应用 。 比如磁悬浮列车中应用到的电动悬浮原理 , 可以通过加强的单边磁场提高悬浮时的浮阻比 , 减小能量损失 , 同时减小对乘客的辐射 。 生活中的冰箱贴多应用价格低廉但磁力弱的钕铁硼材料 , 通过海尔贝克阵列 , 使其可以牢牢吸附 。
上期回顾
NO.235 小怪兽:被奥特曼的激光瞄准 , 我还有救吗? | 正经玩
本文图片
01.Jenny的实验分享如下:
本文图片
02.夏目漱石的实验分享如下:
本文图片
03.我的世界666的实验分享如下:
本文图片
投票时间于1月20日零点截止
票数前 两名 将获得
大师扑克一份
分享赢得纪念品
对于 本期实验 的投稿
我们将在 下期 进行投票
我们将为票数最高的 三位 同学
送去由 人民邮电出版社 出版的
《不可不知的数学知识:10个改变世界的数学公式》
一本
本文图片
数学公式是个很奇妙的东西 , 从最简单的1+1=2 , 到拉开航天航空序幕的齐奥尔科夫斯基公式 , 它们虽然只有几个符号 , 却能够描述大千世界 。 为什么1+1=2 也算一个伟大的发现?为什么万有引力定律是人类思想的一个转折点?为什么等号分隔的两组数字或符号就能够改变世界?你都能在本书中找到答案 。
本书将用有趣的手绘方式 , 把人类历史上最具有影响力的10个数学公式介绍给读者 。 我们将从每个数学公式出现的历史说起 , 用简单易懂的语言带着每一个阅读本书的读者一起 , 跟着人类发展留下的脚印 , 探寻公式背后的哲思 。
推荐阅读
- 用户|海尔李华刚:以用户需求为使命,创三翼鸟的品牌引领
- 智慧|海尔智家:5种家生活开启2022智慧家
- 什么|央视携手海尔智家揭开2022智慧家序幕
- 最新消息|海尔学校筹备明年开始招生 立志成一所世界名校
- 平台|人民日报点赞海尔集团:用数字技术服务美好生活
- 海尔|海尔创客技能大赛让人才脱颖而出
- 先行者|海尔智家:先行者的孤独
- 血液|海尔生物:携手南京市血液中心建"整体智治"数字化血液管理新生态
- 解决方案|华为、海尔与中国移动联合发布5G先进制造全联接场景化解决方案
- 辞任|未来的海尔能保持活力吗







