
老式的脚踏缝纫机应该是一代人的回忆 , 你仔细想过它的原理吗?为了更便捷地使用 , 上百年来聪慧的工程师对这种机器进行不断革新 , 这里就有着很奇妙的数学 。 即使今天已经出现了智能电动缝纫机 , 但处理布料的缝纫方式仍是线的各种组合 , 重新看这些老物件 , 或许会给人们新的启发 。
撰文丨Tony Philips(石溪大学荣誉数学教授)
编译丨Hadron
缝纫机是十九世纪机械发明的奇迹之一 。 据说 , 圣雄甘地曾经称它是“人类为数不多的有用发明之一” 。 这种自动化的工具与打印机或者点钞机不同 , 应用它来处理的最终是实际的材料 , 而非呈现信息 。 在本文中我将从数学层面探索缝纫机和通常被同时提及的绕线器(bobbin winder)的原理:双线连锁缝纫法(Lockstich , 也称为锁式线迹 , 是缝纫机上最常用的一种工艺)在拓扑层面上如何实现 , 以及阿基米德螺旋线形状的凸轮是如何保证在长线轴上均匀绕线的 。
线步拓扑学
最原始的缝纫机使用的是单线链式线迹: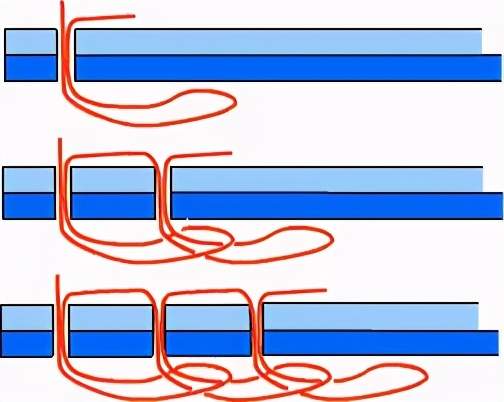
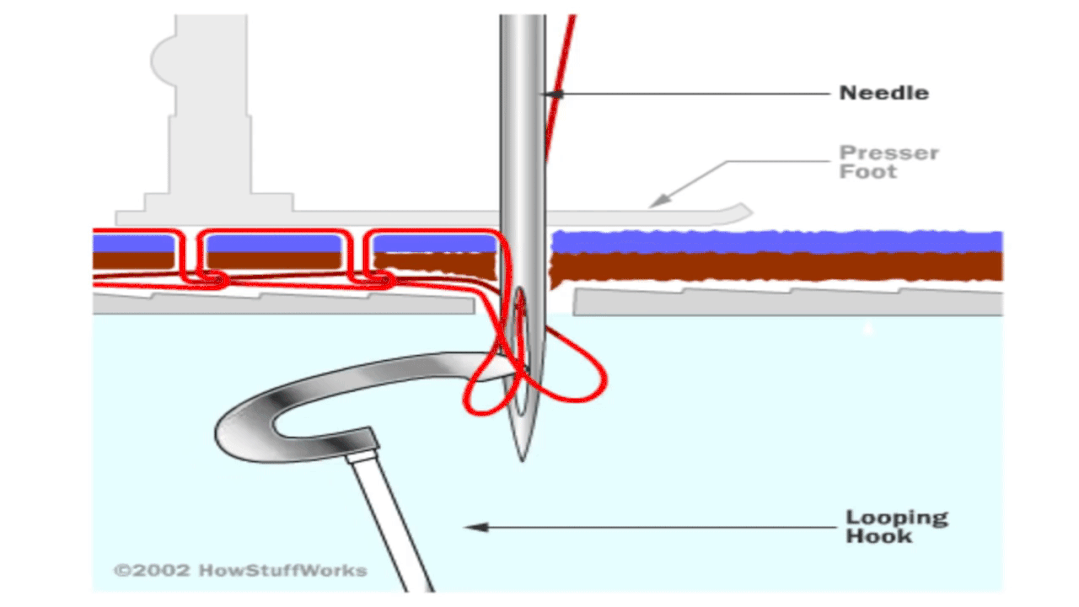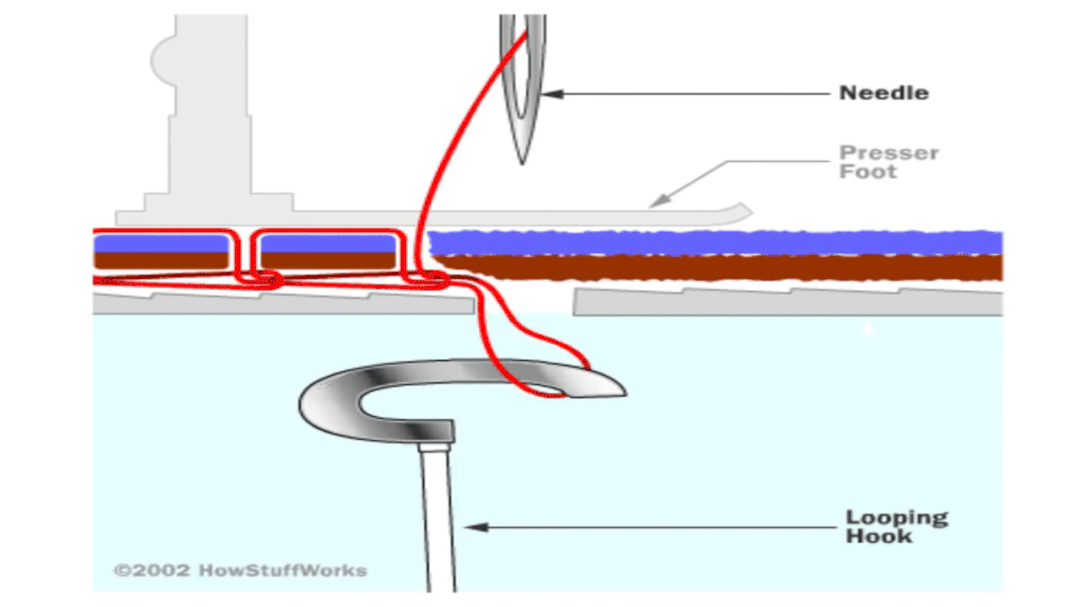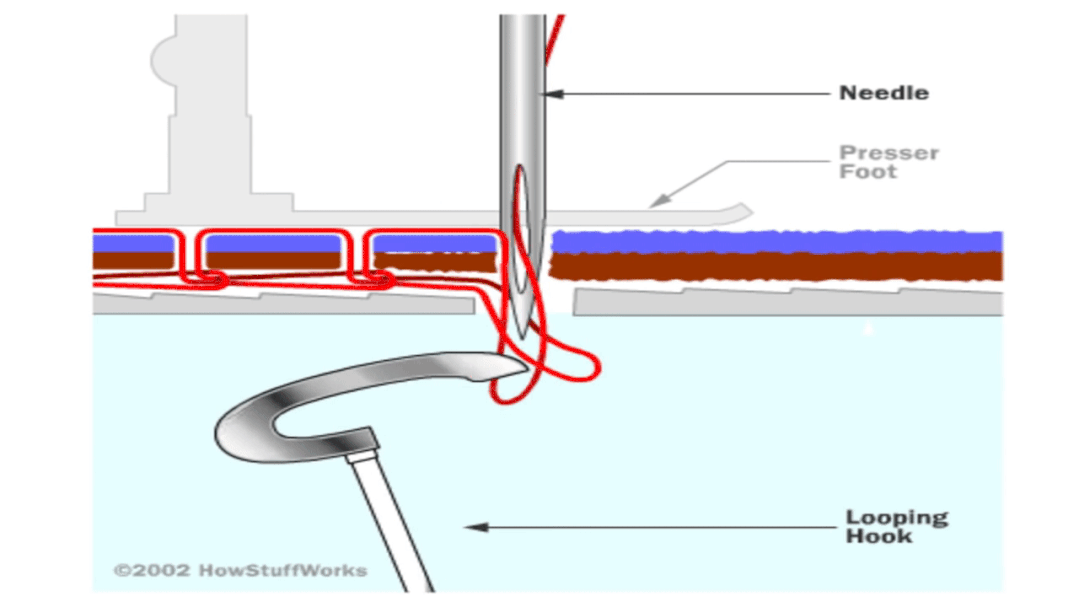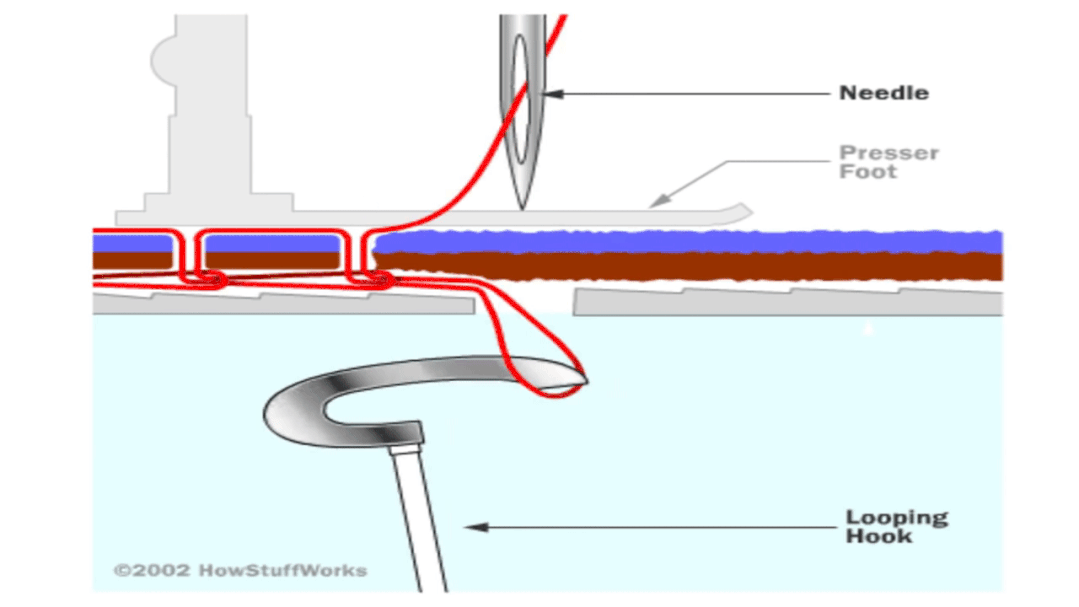
链式线迹缝法:每逢一针 , 一圈丝线都被拖进上一圈线形成的环中 。
链式缝法在拓扑学上不是个难题 , 因为线完全不打结——只需拉动上图的右端线头 , 就足以让整个缝线瓦解 。 对于一些需要容易打开的情况 , 比如家里装满土豆或者狗粮的袋子 , 这种缝法是比较好用 。 但是 , 有的时候这个特性是灾难性的 , 除非你那么想要一件一扯就坏的衣服 。
最早实现锁式缝法的缝纫机大约诞生于1830年至1850年间 , 这种缝纫机用两股线来缝制 。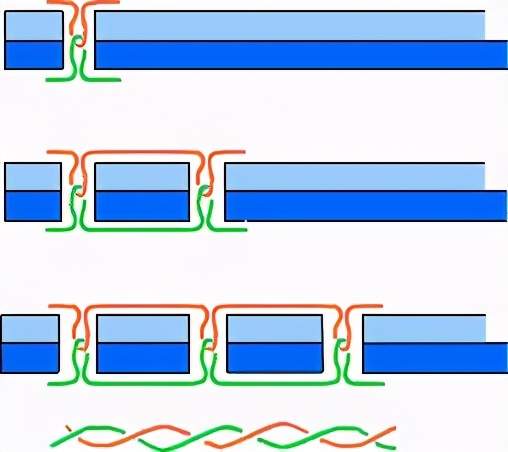
锁式线迹逢法:在每一个针脚处 , 上方的线与下方的线缠绕在一起 , 并且朝向一致 。 如果忽略要缝的布料 , 你会看到两股线均匀地缠绕在一起 , 一股绕着另一股 。
一眼看上去 , 用机器缝出锁式缝法从拓朴学上来说似乎是不可能的 。 缝纫机用两股线来缝接缝 , 而每股线都来自一个线轴——上方的线来自位于机器顶端的线轴 , 下方的线则来自于隐藏在缝纫机内部梭子里的线筒 。 那么问题来了 , 这两股线是如何一圈一圈地缠绕在一起?
答案很简单 , 线筒没有固定在缝纫机上 。 在早期的缝纫机上 , 线筒装在子弹形状的梭子里 , 每缝一针 , 梭子就先前进穿过上线 , 当针抬起后 , 梭子退回 , 这样就完整地绕了一圈 。 梭子在缝纫机中能够自由地穿梭就是实现这种缝法的关键 。 在更现代的缝纫机中 , 线筒被卡在一个光滑的圆形金属梭子中 , 它处于一个固定的位置 , 但不是被完全固定住 , 而是可以转动 。 每缝一针 , 上方线都被挂到金属梭子上 , 随之转动后刚好和下方线缠起来并被拉紧 。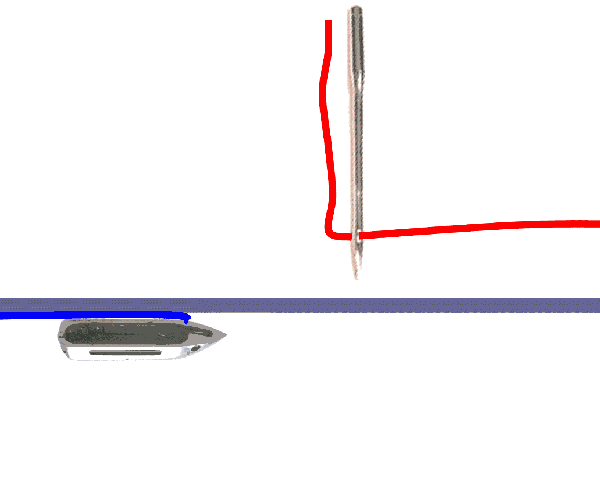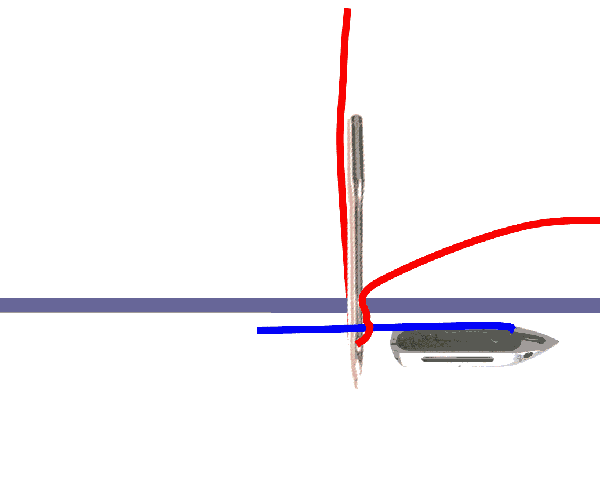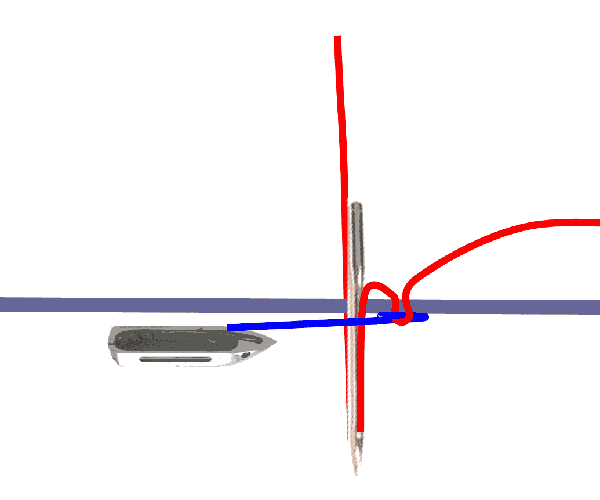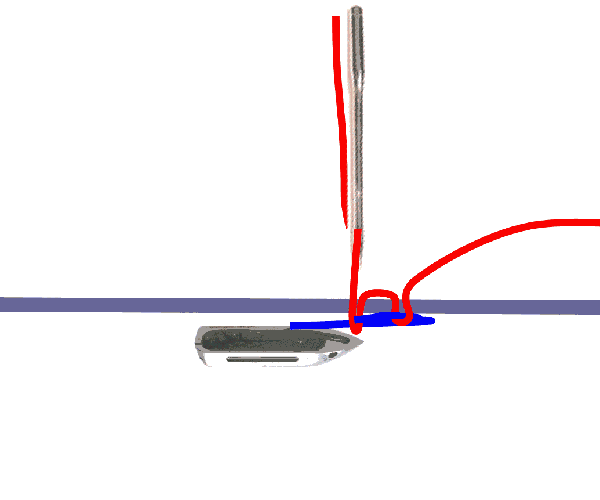
图a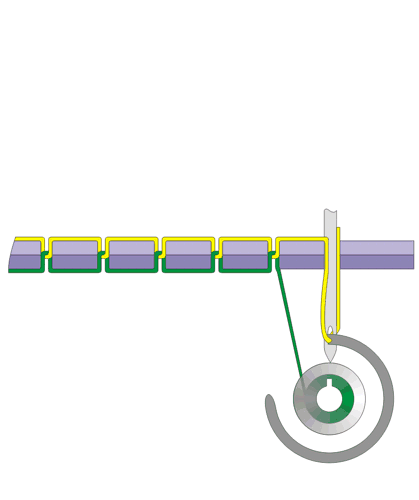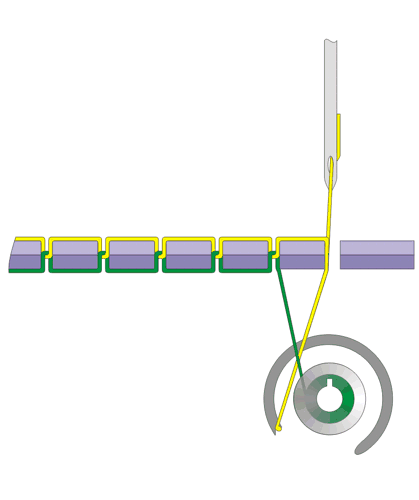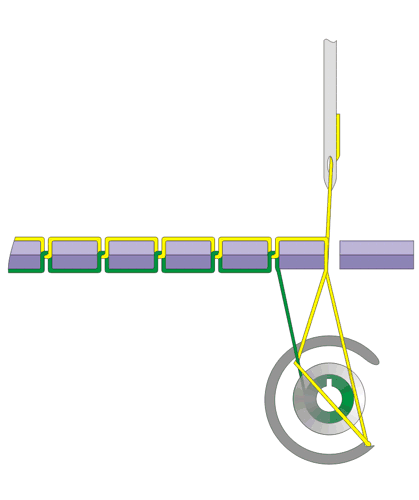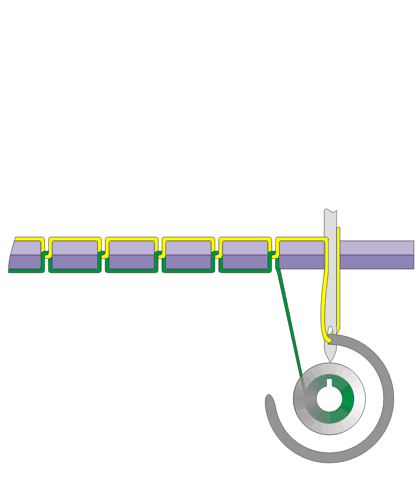
图b
两种实现锁形缝法的方案 。 图a:“振荡梭” 。 每缝一针 , 梭子带着线筒(蓝线)穿过上方线(红色)形成的环 。 图b:“旋梭” 。 线筒(绿线)被封闭在保持固定的圆形光滑梭子里 , 每缝一针上面的线(黄色)被拉向绕梭子一圈 。 在这两种情况下 , 为了保证在拓扑学上是可能的 , 梭子必需在机器内能够自由运动 。
神奇的阿基米德螺旋线
这些有意思的东西我是从前同事 , 也是好友Enrico Giusti(意大利数学家)那里得知的 。 他之前在威尼斯举办的“数学与文化(Matematica e Cultura)”会议的讲座中提到了缝纫机和绕线器 。 这些内容也可以在佛罗伦萨的数学博物馆“阿基米德花园(The Garden of Archimedes)”里找到 。 另一位意大利数学家Franco Conti创建了这个展览 , 想法源于他和Giusti在2000年时出版的Oltre il Compasso: la geometria delle curve(《超越圆规:曲线的几何》)一书 。 博物馆网站上还有这些绕线器的工作机制 。
对于那些不熟悉双线连锁缝纫机的人来说 , 每台机器都不相同 , 因为它们都有各自独特的梭芯——一个嵌在梭子内载着下方线的小线筒 。 为了更方便地将线绕在梭芯里的线筒上 , 每台缝纫机上都有绕线器这样的装置 , 它们通常挨着缝纫机的主轴 , 距离缝纫操作较远的地方 。
左图展示的是经典的缝纫机 , Singer Sphinx Model 27, 1910年制造 。 右图是绕线器的近距离展示 。 Model 27是有振荡梭的设计 。
子弹状振荡梭模型和绕线筒 , 展示的这款长约1.5英寸 。
对于那种圆形旋转梭里面较短的线筒 , 要保证线缠绕均匀通常不是问题 , 缝纫机上的绕线器能让线均匀地抽出来(当然还是建议你盯着点绕线的过程 , 必要时用手调整一下) 。 但是像上图中那种古老型号使用的又窄又长的线筒就不那么好办了:在缠绕过程中 , 需要沿着线筒来回引导线 。 有种非常简单的解决方法 , 即在绕线器上设计一个可动的结构 , 来达到来回运动的效果 。 下图展示了这种简单的机制 , 线可以被引导通过一个转动的、直径与线筒长度相等的环上 , 然后通过固定点连到绕线器 , 但这会导致线在线筒两端堆积 。 在右图中 , 可以看到绿色区域的绕线量是相同长度红色区域的两倍 。 Conti解释了这样做为什么会让线在线筒的两端堆叠 。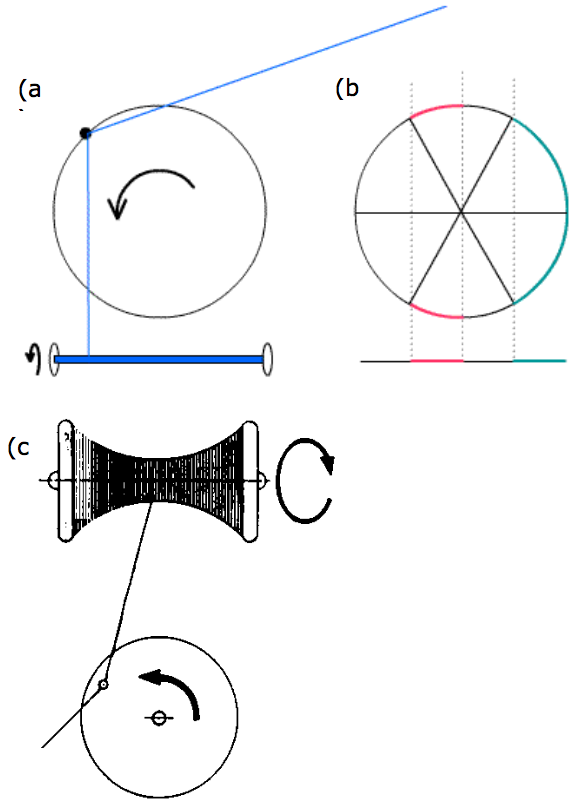
(a)图为实际装置示意图 , 绕线筒绕沿平行纸面方向匀速旋转 , 圆盘沿垂直纸面方向匀速旋转 。 圆盘上黑点对应下的线筒的位置为绕线的位置 。 黑点在线筒上方停留时间的长短决定了绕线量的多少 。 如图(b)所示 , 圆盘均匀转动一圈时 , 绕线筒绿色部分区域在圆盘上对应的圆心角大小是红色部分所示区域对应圆心角大小的两倍 , 因此绿色区域的绕线量是红色区域的两倍 。 由此可见绕线将在线筒两端堆叠 , 结果如图(c) 。
解决方案由这类缝纫机的发明者和后续发展者提出 , 就是在类似于上图的旋转圆盘上安装一个心形的凸轮 , 就像两条阿基米德螺旋拼起来一样 。 (在极坐标轴可以表示为当 0≤θ≤π , r=θ , 当 ?π≤θ≤0 , r=?θ) 。 与之连接的臂杆可以调整以匹配绕线器的长度 。
1868年出版的507 Mechanical Movements收录了这种利用阿基米德螺旋把圆周运动转换成均匀线性运动的装置 。 (507 Mechanical Movements , 《507种机械运动》 , 作者Henry T. Brown是The American Artisan杂志的编辑 , 这份刊物专门刊登工业革命时期机械工程领域的新内容 , 最终Brown将其集合成书 , 出版了21版 。 现在这本书可以在网上查到 , 并有动图 。 )这个缝纫机上的巧妙装置是第96个 , 书中还给出了解释 。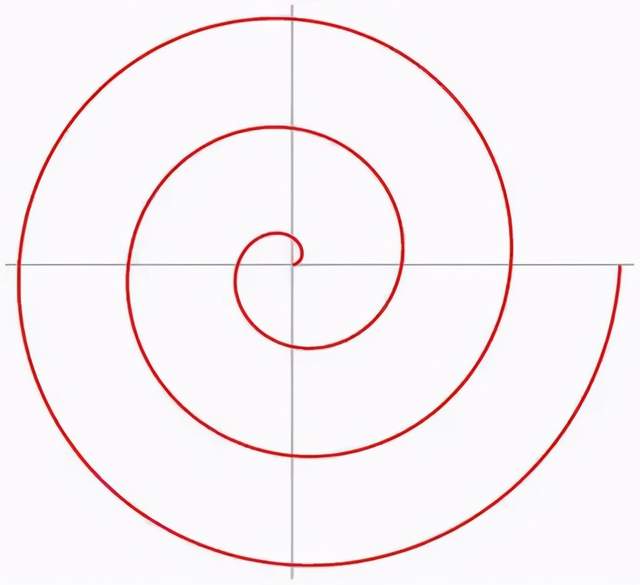
阿基米德螺线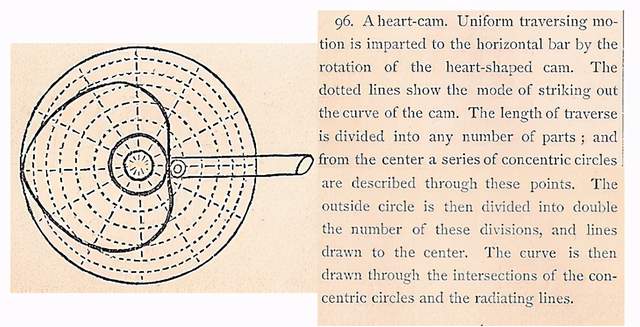
507种机械运动书中记录的心形凸轮
心形凸轮 。 心形凸轮的旋转可以使臂杆得到均匀的横向运动 。 虚线拟合出了心形凸轮的运动轨迹 。 臂杆装置被等分成任意个部分 , 从这些点确定了一系列的同心圆 。 从外圈的最左边的点开始 , 每向中心走一小格的时候 , 同时需要转动等间距的角度 , 逐渐走向中心 。 那么 , 这些同心圆和向外辐射线的交点就是我们希望拟合出来的曲线 。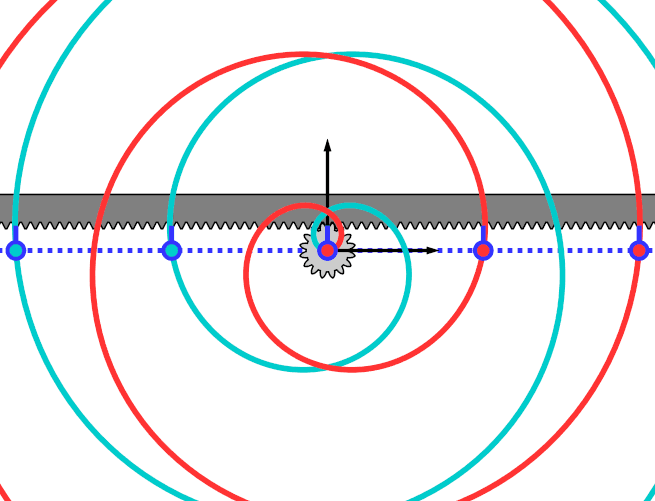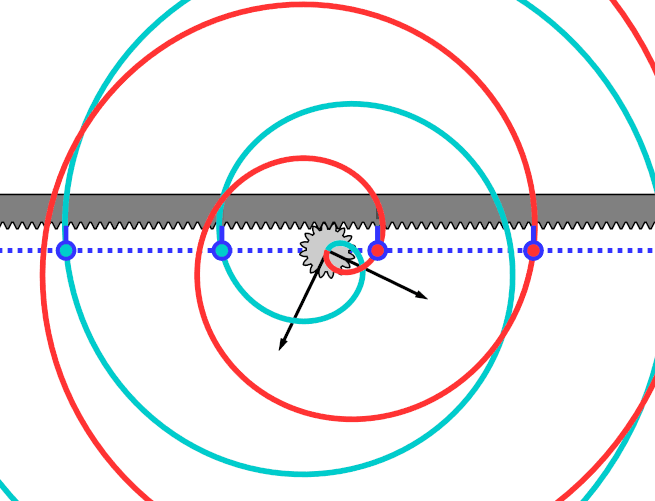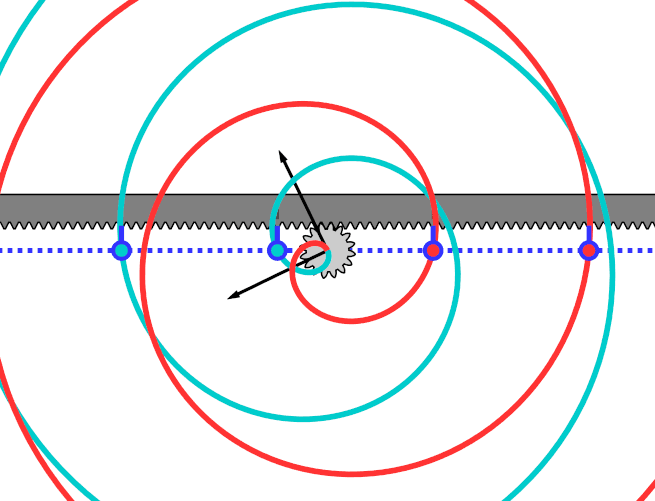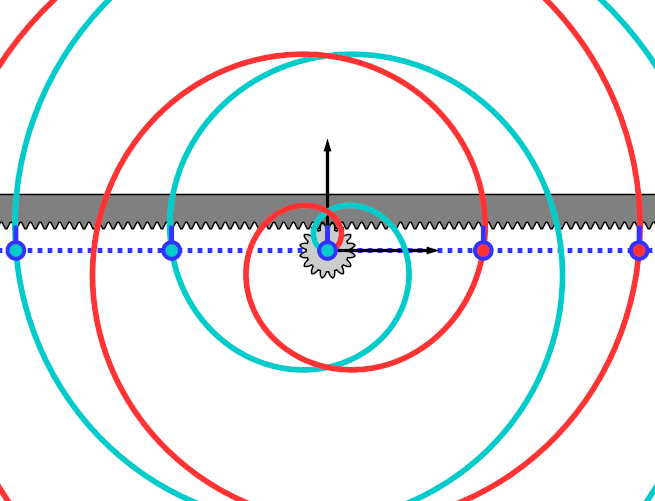
早些年比较火的光盘 , 实际上是由载有信息的条状介质(厚1.6微米)绕制而成的 , 它也是一条阿基米德螺旋线 。 这样做的好处是 , 当光盘匀速旋转时 , 读取信息的激光头只需要匀速地沿光盘做径向运动 , 就可以均匀地读取刻录在条状介质上的信息 , 而且不会间断 。 更古老的留声机的黑胶唱片也是类似的原理 , 它表面的信息载体——刻槽就形成了一条完美的阿基米德螺旋线 。
阿基米德螺线是既作匀速转动又作匀速直线运动而形成的轨迹 。 不同的是 , 有的是垂直旋转轴匀速直线运动 , 如前面提到的凸轮和光盘;有的是平行于转轴的匀速直线运动 , 如阿基米德扬水器 。 据说 , 公元前3世纪 , 阿基米德为了解决用尼罗河水灌溉土地的难题 , 发明了圆筒状的螺旋扬水器 , 后人称它为“阿基米德螺旋” 。 阿基米德螺旋扬水器是最古老的水泵 , 借着螺旋曲面绕着旋转轴做旋转运动 , 将水从低处传输至高处 , 用于农田灌溉 。 凭着它操作简单、结构维修简便 , 流速平稳等优点 , 至今在工业应用中仍有阿基米德螺旋泵的身影 。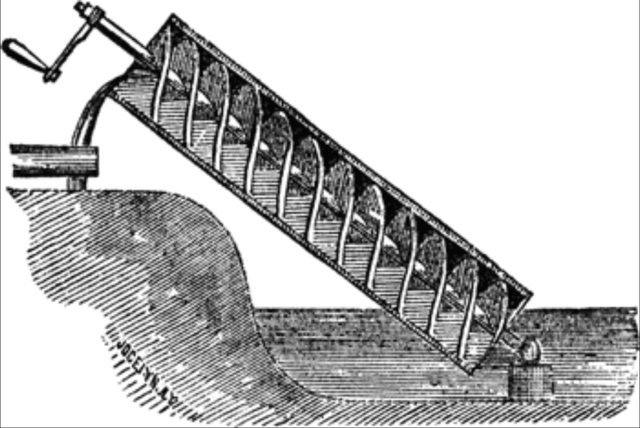
上图所示为阿基米德螺旋扬水器 , 转轴每旋转一圈 , 每个格子里的水都向前推进一个螺距 。
应该注意的是 , 阿基米德螺旋经常与另一种常见螺线——等角螺线(或称对数螺线)混弄 , 它们的区别在于后者旋转是以几何指数递增 , 而阿基米德螺线是恒定的 。 大数学家雅各布·伯努利对这种曲线颇为痴迷 , 相传他要求死后把等角螺线刻在墓碑上 , 结果最终工匠刻成了阿基米德螺线 。
等角螺线
阿基米德螺线 , 这种简洁且深邃的曲线也出现在今天各类工程应用里 , 小到螺丝 , 大到通讯天线 。 技术的魅力在于为人类带来了切实的应用 , 而背后的原理更显自然界的神奇 。 或许你再翻出仍在储藏间角落的缝纫机 , 还能发现过去没注意到的科学道理 。
【缝纫机|那位还在用老式缝纫机打补丁的朋友,可能是个数学小天才】本文图片均来源于网络 。
推荐阅读
- 视点·观察|科技行业都在谈论“元宇宙”,可是它还不存在
- 蛋白|二代新冠疫苗来了!打了一代,还需要它吗?
- 国药|二代新冠疫苗来了!打了一代,还需要它吗?
- 电子商务|员工抱怨亚马逊太冷酷:工伤后得不到赔偿 还不让休假
- OriginOS|当硬件驱动力逐渐放缓,手机还能更快吗?
- Pro|价格相差1000块钱 买小米12还是小米12 Pro?很多人选错了
- 硬件|上线两年用户破两亿,腾讯会议还能做什么?
- IT|保费涨80% 专车司机还是爱特斯拉
- 视觉|超高色准打破行业天花板,创维S82还原真实世界
- 智能汽车|瞄准2022的靶心 智能汽车还要深挖潜力







