宇称不守恒 , 这是一个让许多中国人既熟悉又陌生的词语!
熟悉 , 是因为这是全球华人的第一个诺贝尔奖 , 我们的教科书和媒体会经常提到这个也是很自然的事情;陌生 , 是因为大多人除了知道杨振宁和李政道发现了它以外 , 完全不知道这个宇称不守恒到底在说啥 。
另外 , 跟前沿理论物理的一大堆让人懵圈的专业术语相比 , “宇称不守恒”这五个字看起来还是很亲民的 。 毕竟我们中学时代就学过能量守恒、动量守恒 , 对守恒的概念还是很熟悉的 , 而“宇称”听起来应该和宇宙的某种对称性有关 。 然而 , 宇称到底是什么呢?为什么它不守恒?为什么宇称的不守恒会让科学界如此震动 , 以至于杨振宁和李政道在1956年6月提出了宇称不守恒 , 1957年的诺贝尔物理学奖立刻颁给了他们?
没错 , 宇称确实是指一种对称性 , 要想理解宇称不守恒为什么这么重要 , 就要先理解为什么对称性这么重要 。
那么 , 对称性到底有多重要呢?这么说吧 , 如果没有对称性作指导 , 爱因斯坦不可能发现相对论 , 当代的理论物理学家们会像失去了灯塔一样集体在黑暗里抓瞎 。 物理学大师费曼曾经说过 , 如果让他选择一句话来概括现代科学最重要的发现 , 他会选“世界是原子组成的” 。 许多当代最著名的物理学家们认为 , 如果有机会再选一句 , 那么所选的将是“对称性是宇宙规律的基础”这句话 。
01什么是对称?
一提到对称 , 许多人脑海里会浮现类似天安门这种严格左右对称的建筑 , 或者六个瓣的雪花 , 镜子里帅帅的自己 , 亦或者是纯粹的圆形、正方形、正六边形这样的几何图形 。
本文图片
没错 , 这种几何里的对称是我们最容易想到的 。 仔细想一下这些对称 , 我们会发现它们有的是以中间一根轴对称(天安门) , 有的是围着一个点旋转对称(雪花、圆形、正方形) , 还有的是相对镜子里的镜像对称 。 当然 , 天安门的那种轴对称你也可以认为它是在天安门中间插了一面镜子 , 不过这个不是重点 , 我的重点是:对称的标准可以是多样的 。
对称性的精确数学定义涉及到不变性的概念:如果一个几何图形在某些操作下保持不变 , 我们就说这个图形在这些操作之下具有某种不变性 。
一个圆无论你旋转多少度 , 这个圆看起来还是那个圆 , 它没有任何变化 , 我们就说圆这个图形在旋转这个操作下具有不变性 , 简单的说就叫圆具有旋转不变性 。 同样的 , 我们用镜子去照一个圆 , 镜子里的图形依然是一个圆形 , 通过镜子照的这个过程我们可以称之为反射 , 那么 , 圆也具有反射不变性 。 可以想象 , 三角形、正方形乃至任何几何图形在镜子里依然是这样的图像 , 所以它们都具有反射不变性 。
这是我们辨别对称常用的思维 , 但是物理学家们却更喜欢另一种思维 。
以旋转不变为例 , 我们判断一个图形是否具有旋转不变性 , 是去尝试着把这个图形给转一下 , 看看他跟以前还是不是一样的 。 这是观察者不动而图形动 , 但是物理学家们更喜欢使用另外一种方法:图形不动 , 观察者动 。
什么意思呢?比如物理学家们判断一个圆形是否具有旋转不变性 , 他不是去旋转这个圆看他变没变 , 而是去旋转观察者 , 让观察者从不同的角度去看这个圆 , 看他们看到的是不是同样的圆 , 如果是一样的就说圆具有旋转不变性 。 因为运动具有相对性 , 所以观察者不动旋转圆和圆不动旋转观察者本质上并没有什么区别 。 物理学家们的这种处理方法会使在处理复杂问题的时候变得简单很多 , 后面你就能体会到了 。
上面我们说的对称都是只几何图形的对称 , 但是物理学家们并不关心几何图形 , 他们关心的是物理定律 , 也就是是物理定律的对称性 。 初次听到这个词很多人可能会感觉到奇怪 , 几何图形对称好理解 , 什么叫物理定律的对称性呢?物理定律不是一堆公式么 , 为什么会去考虑他们是否对称的问题?
02物理定律的对称
要理解物理定律的对称性 , 我们就要把脑袋里几何图形对称的那个图景忘掉 , 回到对称更一般的数学定义上来 。 我们上面也说了 , 对称性的精确数学定义会涉及到不变性这个概念:如果一个几何图形在某些操作下保持不变 , 我们就说这个图形在这些操作之下具有某种不变性 。
我们把上面的几何图形换成物理定律 , 就可以很自然的得到一个物理定律是否对称的判断标准:如果一个物理定律在某些操作下保持不变 , 我们就说这个物理定律在这些操作下具有某种不变性 。
还是以旋转操作为例 , 我们来看看牛顿运动定律在旋转这个操作下是否保持不变 , 也就是说看看牛顿运动定律是否具有旋转不变性 。 答案是很明显的 , 比如一个苹果从树上落下 , 我们不管是从树下仰视 , 从树上俯视 , 还是从远方平视 , 甚至是从飞机上看 , 我们都会看到苹果的下落过程符合牛顿的运动定律:苹果朝着地心的方向加速飞去 。 一个俯视苹果下落的牛顿和一个仰视苹果下落的牛顿不可能总结出两个运动定律出来 , 这就是说牛顿定律符合旋转不变性 , 也就是说牛顿定律在旋转这个操作下具有对称性 。
我们想想 , 不止是牛顿定律 , 我们现在发现的任何定律都符合旋转不变性 , 也就是旋转下的对称性 。 麦克斯韦的电磁学也好 , 爱因斯坦的相对论也好 , 量子力学也好 , 如果我们从不同的角度去看他们就会得到不同的电磁学规律、相对论那还得了?
我们再往深层想一下 , 旋转不变性的本质其实是空间的各向同性 。 也就是说 , 只要空间在各个方向上都是均匀的 , 都是一样的 , 不存在空间这边密度大一点那边密度小一点 , 那么观察者从不同方向看到的物理定律就肯定是一样的 , 即这些定律肯定具有旋转不变性 。
在这里 , 我们看到了物理定律的旋转对称性居然和空间本身的性质联系起来了 , 有没有隐隐约约感觉对称性不只是看起来好看 , 好像还挺有用呢?别急 , 这才看到对称性威力的冰山一角 , 对称性的威力还大着呢~
03诺特定理
物理学家研究对称性绝不是图好玩 , 是因为对称性里蕴含了巨大的能量 。 要充分理解对称性的威力 , 我们必须先了解一个核弹级别的定理:诺特定理 。
诺特定理 , 顾名思义是一个叫诺特的科学家发现的定理 , 这个科学家叫埃米·诺特 , 是位著名的女科学家 , 被爱因斯坦形容为数学史上最重要的女人 , 还被称为现代数学之母 。 诺特在数学上的成就我这里不多说 , 她在物理学上最重要的成就就是发现了现代物理学灯塔 , 让现代物理学家们不再抓瞎的诺特定理 。
本文图片
诺特定理的表述非常简单 , 就一句话 , 但是内容非常深刻 , 它说:物理学里的连续对称性和守恒定律一一对应 。
我先不做过多的说明 , 让大家先把思路捋一捋 , 这句话里的每一个字我们都懂 , 它要表达的意思也非常清楚 , 但是这到底意味着什么?
对称性和守恒定律一一对应 , 那就是说每一个对称性都有一个守恒定律跟它对应 , 每一个守恒定律也有一个对称性跟它对应么?那岂不是说我熟悉的能量守恒定律 , 动量守恒定律也都对应了某个对称性?那上面的旋转对称 , 反射对称又对应了什么守恒定律呢?如果它们之间真的是这样一一对应的 , 那么以后我只要在实验里发现了新的守恒量 , 就等于发现了一个新的对称性么?这太不可思议了……
没错 , 上面想的都没错 , 诺特定理说的清清楚楚明明白白 , 没有任何歧义 , 就是这样!
另外 , 关于诺特定理里连续对称性的连续 , 我稍微说明一下:在经典力学里 , 像旋转对称 , 我们可以旋转任意的角度 , 这显然是个连续的对称 , 而镜像对称则要么是镜里要么是镜外 , 只能取两个值 , 这是不连续的 。 在经典力学里 , 守恒定律是跟连续对称性一一对应的 。 但是到了量子力学这里 , 压根就没有连续的东西 , 一切都是量子化的 , 所以这种差异就没有了 。 因此 , 在量子力学里 , 即便是镜像这种不连续的对称也有相应的守恒定律 。
为了让大家对诺特定理有更深刻的理解 , 我们先来看看几个常见的例子 。
04能量守恒定律的对称性
诺特定理说对称性和守恒定律一一对应 , 那么就先从我们最熟悉的能量守恒定律开始 。 既然能量守恒 , 那么按照诺特定理就有一种对称性与之对应 , 是什么对称性呢?
这里我不卖关子了 , 直接告诉大家 , 跟能量守恒对应的这种对称性叫时间平移不变性 。 什么叫时间平移不变性 , 平移就是时间流逝移动的意思 , 说得再通俗一点就是:我今天做实验跟明天做实验遵循同样的物理定律 。
噢 , 这下子秒懂了!有人说这不是废话么 , 一个物理定律如果他今天成立明天不成立 , 那还叫什么定律 , 那我们要这样的定律还有个锤子用?没错 , 吐槽的一点没错 , 物理学家们千辛万苦的寻找各种物理定律 , 为的就是利用这些定律预测物体未来的运动情况 , 你如果跑来告诉我这个定律只有这一刻有效 , 下一刻就失效了 , 也就是没有时间平移不变性 , 那我们还预测个啥啊?
所以 , 显而易见的 , 我们目前所有的物理定律都是符合时间平移不变性的 , 明白了这一点 , 你就知道为什么能量守恒定律的适用范围这么广了吧?因为诺特定理告诉我们 , 只要物理定律是时间平移不变的 , 那么他就肯定能量守恒 , 而时间平移不变看起来这么强 , 所以能量守恒也就这么强了 。
现在这个关系是对应起来了 , 但是大部分人脑袋里肯定还是懵的:为什么能量守恒定律就是跟时间平移不变性对应 , 而不是跟其他的对称性对应呢?具体的证明过程比较复杂 , 这里就不说了 , 有兴趣的自己去查资料 , 我这里提供一个简单的思路让大家直观的感受一下为什么如果没有时间平移不变性 , 能量就不守恒了 。
假设物理定律不遵守时间平移不变性 , 这一秒的定律跟下一秒的定律不一样 。 那我把一块石头往上抛 , 让它刚好一秒钟达到最高点然后它开始下落 , 我假设下落时的定律让同样大小的引力能够产生两倍于上抛时候的加速度 , 那时候下落到出发点的时候它的速度肯定比上抛的时的初候速度更大 , 也就具有更大的能量 。 那么 , 在抛一个石头的过程中它就凭空创造了能量 , 所以能量显然就不守恒了 。
理解了能量守恒对应时间平移不变性之后 , 后面两个熟悉的守恒我就直接说结果了:动量守恒对应空间平移不变性(空间平移不变就是说物理定律在北京和在上海都一样 , 在不同的空间物理定律相同) , 角动量守恒对应于我们上面说的旋转不变性 。 有了这种概念以后 , 知道了能量、动量、角动量守恒定律不过是一种对称性的体现之后 , 我相信你不会再怀疑对称性在物理学的重要性了 。
那么 , 镜面的反射对称呢?物理定律是否遵循反射对称呢?如果遵循反射 , 那么它对应的守恒定律又叫什么呢?
【物理|宇称不守恒到底说了啥?】
05宇称不变性
做了这么多铺垫 , 我们文章的主角——宇称 , 也该出场了 。 没错 , 跟镜像反射对称 , 也就是左右对称相对应的这个守恒量 , 就是宇称 。 宇称也跟物体的质量、电荷一样 , 是描述基本粒子性质的一个物理量 。
所以 , 我们说物理定律的宇称不变性 , 其实就是说物理定律在经过镜面反射对称处理之后依然保持不变 , 简单的说就是镜子里的世界跟外面的世界遵循同样的物理定律 。

本文图片
怎么通俗的理解这个事?举个例子 , 我们每个人都有照镜子的体验 , 因为人体的特殊对称性 , 镜子里的人看起来跟镜子外面的人一模一样 , 但是左右颠倒了 。 也就是说 , 镜子外面的人动一下左腿 , 你会感觉到镜子里面的人动了一下右腿 。 如果这时候外面还有一个足球 , 镜子外面的人用左腿提了一下足球 , 这个足球会按照牛顿运动定律被踢开 , 同时我们会看到镜子里面的人会用右腿把把这个足球朝另一个方向踢开 , 现在问题的关键是:镜子里面的人踢足球这个过程是否满足牛顿运动定律?
如果也满足牛顿运动定律 , 那我们按照定义就可以说牛顿运动定律在镜面反射对称下具有不变性 , 也就是具有宇称不变性 , 那这个过程就宇称守恒 。
可以想象一下 , 如果现实生活中你真的有一个一模一样的双胞胎 , 这个双胞胎完全按照你镜子里的样子站立 , 按照你镜子里的样子用右腿踢那个球 , 双胞胎的球和镜子里的球会按照一样的轨迹运动么?
答案是肯定的 , 镜子里的世界跟你一样遵循牛顿运动定律 , 根据牛顿运动定律根本无法区分镜子里面和外面的世界 。 如果你有魔力把镜子里的人和球都抠到现实世界里来 , 你会发现他跟你除了左右相反之外 , 他踢球的过程跟你平常的感觉是一模一样的 , 踢出去的球依然是一条优美的抛物线 。
这也就是说 , 牛顿运动定律具有严格的宇称不变性 , 按照牛顿运动定律发生的过程严格宇称守恒 。 其实 , 不止是牛顿运动定律 , 在四大基本相互作用力里 , 电磁力、引力、强力的物理规律都具有宇称不变性 , 由它们支配的过程都宇称守恒 。
但是 , 剩下的那个弱力呢?
06从宇称守恒到宇称不守恒
宇称 , 也就是镜面反射对称 , 在我们日常生活里实在是太常见太熟悉了 。 镜子里的世界跟镜子外的世界比也就是左右互换了一下 , 镜子外顺时针旋转的东西在镜子里面在逆时针旋转而已 。 我们的直觉告诉我们上帝应该是公平的 , 他没有任何理由偏爱左边或者右边 , 相对论的成功更是极大地加深了这种思想 。
所以 , 宇称不变性 , 也就和其它几个最基本的不变性(比如时间平移不变、空间平移不变、旋转不变等等)一样 , 被物理学家们视为最基本的规律 。 视为最基本的意思就是说 , 如果科学家们发现了有什么现象似乎违反了这个规律的时候 , 大家首先的反应不是这个规律有问题 , 而是还有其他没有考虑进来的因素 。 这里最明显的就是时间平移不变性对应的能量守恒了 , 有很多次物理学家们发现某个物理过程不满足能量守恒 , 他们不会怀疑能量守恒出了问题 , 而是去找有什么新粒子或者新现象没有被发现 , 然后后来他们就真的找到了这样的新粒子新现象 , 然后顺便去斯德哥尔摩旅了个游 , 这一招屡试不爽 。
宇称不变性跟他的几个兄弟一样 , 一路帮助物理学家们过关斩将 , 所向披靡 , 没有人怀疑宇称守恒的“忠心” 。 直到有一天 , 从中国走出来了两个天才物理学家:杨振宁和李政道 。
本文图片
首先我们要清楚 , 向物理世界中这些最基本最基础最“显而易见”的东西开炮是需要极大的勇气和极高的洞察力的 , 这种最底层的根基一旦被动摇了 , 物理学的世界接下来肯定就要地动山摇、天翻地覆 。 粗算一下 , 上一次对如此基础的概念开炮还是爱因斯坦对牛顿绝对时间和绝对空间的抨击 , 以及量子力学的革命 。
两朵乌云引发相对论和量子力学革命的故事我们已经很熟悉了 , 那么 , 杨振宁和李政道为什么要向宇称守恒这么基本的东西开炮呢?这个原因还得从弱相互作用 , 也就是常说的弱力开始说起 。
07弱相互作用
我们在自然界发现的所有作用力最终都可以归结为这四种:引力、电磁力、强力、弱力 。 引力和电磁力我们很熟悉 , 强力和弱力都发生在原子核里面 , 我们平常接触不到 。 强力简单的说就是粘着质子、中子、夸克不让原子核分崩离析的那种力(不然的话 , 质子都带正电 , 它们之间同性电荷产生的排斥力早就把原子核给拆了) , 弱力是造成放射性原子核衰变的那种力 , 就是中子变成质子 , 质子变成中子那个过程中的力 。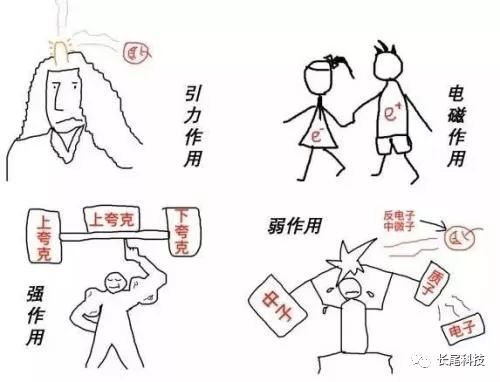
本文图片
弱力出现最典型的一个场景就是β衰变 。
我们都知道原子核是由质子和中子组成的 , 元素周期表里的那个元素的排序(所谓的原子序数)就是按照质子数来排的 。 然而 , 原子核内的质子和中子并不是一直固定不变的 , 在一定条件下 , 质子可以变成中子 , 中子也可以变成质子 , 这个相互变化的过程就β衰变 , 而在这个过程中发挥作用的就是弱相互作用力 , 即弱力 。
最早描述弱力的是费米的理论 , 而这个费米 , 正是杨振宁和李政道的导师 。
08θ-τ之谜
在20世纪四五十年代 , 科学家们在宇宙射线里探测到了许多新的粒子 , 这些粒子并没有在理论中被预言 , 因此被称为“奇异粒子” 。 由于宇宙射线有许多人为不可控的因素 , 为了更好的研究 , 人们开始自己制造粒子加速器 。 粒子加速器听起来很高大上 , 但是大家的使用方法其实很简单粗暴:就是把一些粒子加速到很高的速度(因此具有很高的能量) , 然后把它们当枪使 , 让这些高能粒子去撞各种东西 , 看看能不能撞出一些新东西出来 。
不过 , 虽然手法简单 , 但是效果却非常显著:科学家们撞出了一堆稀奇古怪的“奇异粒子” , 而在这些粒子当中 , 物理学家们最感兴趣的就是θ和τ粒子 。 它们有一些非常奇特难解的特性 , 被当时的物理学家们成为“θ-τ之谜” 。
θ和τ这两种粒子的生命非常短 , 很快会衰变成其他的粒子 , 物理学家们也是通过观察衰变之后东西才推测它们的存在 。 它们奇怪的地方就在于:θ粒子在衰变的时候会产生两个π介子 , 而τ粒子在衰变的时候会产生三个π介子 。
有人会说这有什么奇怪的?一个粒子衰变产生两个那个叫啥π介子的东西 , 另一个产生三个 , 这不是很稀松平常的事么 , 难道粒子衰变生成几个介子还要受法律约束不成?
没错 , 单纯这有看 , 确实没什么奇怪的 。 但是 , 随后人们就发现 , θ和τ这两种粒子无论是电荷、自旋还是质量都一模一样 , 这哥俩无论怎么看都像是同样一个粒子 , 但是它们的衰变结果却不一样 , 这就尴尬了 。
更为尴尬的是 , 澳大利亚的物理学家达利兹仔细的研究了这两个粒子 , 利用当时普遍被接受的物理定律去做了一个计算分析 , 结果表明θ和τ的宇称数不一样 , 因此不可能是同一种粒子 。
当时的局面是 , 有人认为θ和τ是不同的粒子 , 有人认为他们是相同的粒子 , 但是认为它们是相同粒子的人也无法解释为什么它们的衰变结果和宇称数不一样(也就是宇称不守恒) 。 其实 , 当时一些科学已经注意到宇称守恒的成立与否是一个重要的方向 , 但是由于对称性在理论物理里实在太重要了 , 要去质疑它们要不是极聪明就是极蠢 。 另外 , 关于宇称的定律在之前的粒子物理里一直都用的很好 , 因此只要提出宇称不守恒的想法 , 很快就会碰到互相抵触的地方 。
如果杨振宁和李政道认为宇称不守恒是解开θ-τ之谜的关键点 , 那就得先得把那些相互抵触的问题都解决掉 , 并且还要解释为什么之前的各种相关现象并不违反宇称守恒 。
当然 , 他们做到了!
09弱相互作用下的宇称不守恒
在前面我们就提到了 , 基本相互作用力里的强力和弱力都是在原子核发生的 , 因此 , 这两种力很容易搅和在一起 。 有些物理学家即便感觉宇称可能不守恒 , 但是一旦他们认为宇称在强力和弱力下都不守恒 , 接下来肯定会碰到满头包 。
杨振宁和李政道敏锐的发现了这一点:把原子核黏在一起的是强力 , 原子核发生衰变是弱力 , 如果我们把这两个过程的对称性分开来看 , 也就是说 , 假如我只认定宇称在强相互用力中守恒 , 而在弱相互作用力中不守恒 , 那θ-τ之谜看起来就容易多了 。
把强、弱相互作用力区分讨论宇称性 , 这是一个很美妙的想法 。 如果弱相互作用下宇称不守恒 , 那么θ和τ粒子就可以看做同一个粒子不同衰变方式 , 于是杨振宁和李政道就把目光锁定到弱相互作用去了 。 因此 , 虽然θ和τ粒子的衰变过程也是弱相互作用 , 但是这种奇异粒子的弱相互作用我们了解有限 , 既然要研究弱相互作用 , 那当然是研究我们最熟悉的弱相互作用了 。 那么 , 我们最熟悉的弱相互作用是什么呢?大声说出来:
β衰变!β衰变!β衰变!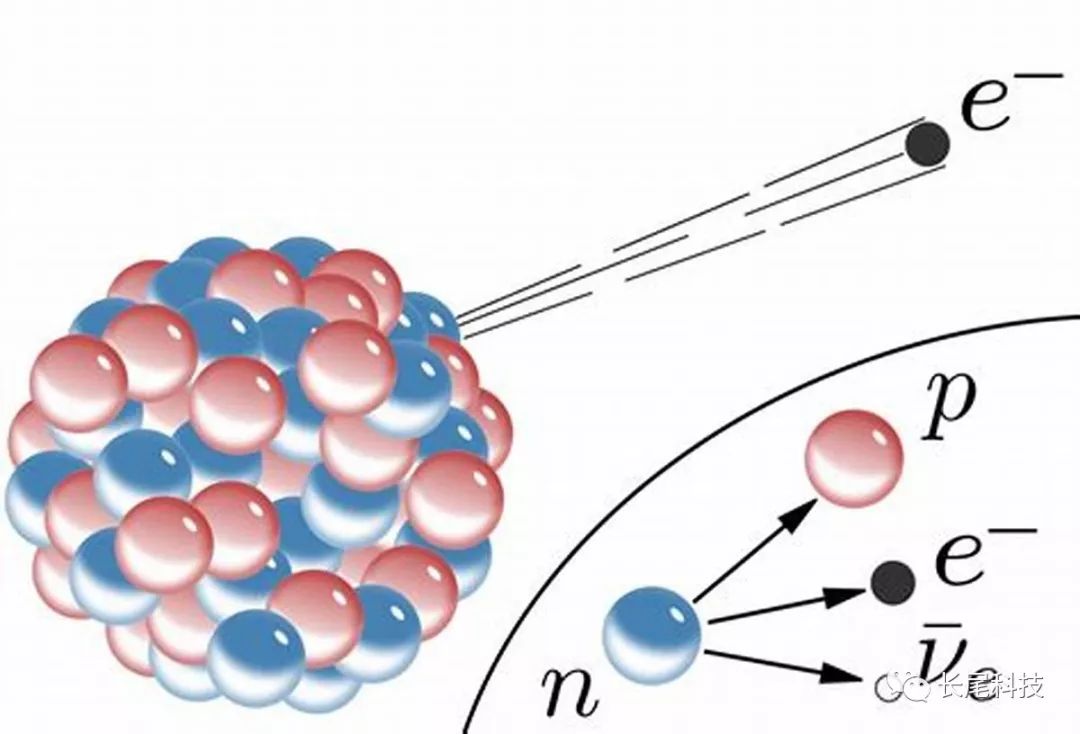
本文图片
答案当然是β衰变 , 所以 , 杨、李二人立马就对过去已有的各种β衰变进行计算考查 , 结果他们发现:在过去所有的β衰变实验里 , 实验结果跟β衰变中宇称是否守恒完全没有关系 。 这是一个令人震惊的结果 , 也就是说 , 在过去的那些有弱相互作用力参与的β衰变实验里 , 宇称守恒与否并不会影响他们的实验结果 , 所以杨振宁和李政道的想法并没有被过去的实验证伪 。
当然 , 也没有被证实 。
后来 , 杨振宁这样描述他们对这个结果的反应:长久以来 , 在毫无实验根据的情况下 , 人们都相信弱相互作用下宇称守恒 , 这是十分令人惊愕的 。 但是 , 更令人惊愕的是 , 物理学如此熟知的一条时空对称定律面临破产 , 我们不喜欢这种前景 , 只是因为试图理解θ-τ之谜的其他各种努力都归于失败 , 我们才不得不考虑这样一种情景 。
现在新的问题来了:既然β衰变是典型的弱相互作用 , 那么为什么我们之前做的那么多β衰变的实验都刚好跟宇称守恒无关呢?经过一番苦思冥想之后 , 杨、李发现了问题的关键:要想用实验检验弱相互作用中宇称是否守恒 , 必须测量赝标量(这是跟核的自旋和电子的动量相关的一个物理量 , 有个印象就行) , 而之前的β衰变实验都没有测量这个 , 所以实验结果就跟宇称是否守恒完全无关 。
认识到这一点之后 , 杨振宁和李政道就重新设计了几个可以检验宇称是否守恒的实验 , 并把具体的实验方法和之前的分析都写进那篇非常著名的论文《在弱相互作用中 , 宇称是否守恒?》中去了 , 然后投给了《物理评论》 。 但是 , 等论文发表的时候 , 论文题目却被杂志的编辑改成了《对于弱相互作用中宇称守恒的质疑》 , 原因是编辑认为一篇论文的标题不应该是一个问句 , 虽然杨振宁认为前者要好得多 。
本文图片
论文发表之后 , 虽然他们在文章里对“弱相互作用力下宇称不守恒”的问题做了很详尽的讨论 , 还提出了一些可以检验的实验办法 。 但是 , 由于宇称守恒过去在各个方面表现得实在是太好了 , 而且这些实验也都不是那么简单的 , 所以他们的论文一开始并没有引起什么热烈的反应 。
10实验女王吴健雄
当时想请一位实验物理学家来做验证宇称是否守恒的时候可不是那么简单的事 , 实验物理学家考虑的是:是否值得去做一个实验来验证宇称是否守恒?杨振宁和李政道虽然提出了几个具体的实验方案 , 但是这些实验都非常困难 , 并且 , 当时物理学家的眼里 , 宇称守恒是绝对可靠的 , 做这样的实验几乎就等于白费精力 。
这种想法在当时是极为主流的 。
有一个叫拉姆齐的实验物理学家后来也想做验证宇称是否守恒的实验 , 费曼告诉他“那是一个疯狂的实验 , 不要再上面浪费时间” , 他还以10000:1来赌这个实验不会成功 , 后来改成了50:1 , 但是由于橡树岭实验室不支持 , 所以拉姆齐只得作罢 。 当宇称不守恒被实验证明之后 , 费曼倒是很守信的开了一张50美元的支票给拉姆齐 , 算是给拉姆齐的一个安慰奖 。 以眼光毒辣 , 被称为“上帝之鞭”“物理学的良心”的泡利听说吴健雄在做这个实验之后 , 他说他愿意下任何赌注来赌宇称一定是是守恒的 , 后来他自己也开玩笑说幸好没有人跟他赌 , 不然他就得破产了(不知道这些物理学家怎么这么喜欢赌博 , 应该打110和911叫警察全抓起来~) 。 最严重的是朗道 , 朗道不仅自己公平批评质疑宇称守恒的想法 , 他有个叫沙皮罗的学生在研究介子衰变的时候也觉得宇称应该不守恒 , 写了篇论文给朗道审阅 , 朗道直接给他丢一边去了 。 几个月后杨振宁和李政道发表了宇称不守恒的论文 , 接着吴健雄用实验做了证明 , 第二年还去斯德哥尔摩捧回了诺贝尔奖 , 朗道这才追悔莫及 。
当然 , 我们也不能说如果朗道没有无视沙皮罗的论文 , 苏联就会先发现宇称不守恒 , 然后先得到一个诺贝尔奖 。 因为当时质疑宇称守恒的人很多 , 但是光质疑没用 , 原因我们上面也说了 , 你从宇称不守恒出发 , 一出门就得到处碰壁 。 杨振宁和李政道是极为敏锐的意识到在宇称守恒这个问题上要把强相互作用和弱相互作用分开 , 把目光锁定在弱相互作用之后他们去全面审查所有的β衰变实验 , 然后发现过去的β衰变实验跟宇称是否守恒无关 , 再接着他们发现了这个无关跟所谓的赝标量有关 , 于是他们设计包含测量赝标量的实验 , 并得到了吴健雄的鼎力支持(想想拉姆齐的实验 , 橡树岭实验中心都不支持它 , 你就知道吴健雄的支持是哪种力度的支持了)才得以完成 。 这所有的环节缺一不可 , 并不是简单你以为宇称不守恒就能去斯德哥尔摩一游的 , 诺贝尔奖不是这么好拿的 。
吴健雄的天才在这里不是表现在设计了多么巧妙的实验 , 而是表现在大环境对验证宇称是否守恒如此不利的情况下(想想费曼、泡利、朗道都是什么级别的人物) , 她全力支持杨振宁和李政道的想法 。 她不仅要做实验 , 还要迅速做赶快做 , 要赶在其他的实验物理学家意识到这个实验的重要性之前做出来 。 为此 , 她把取消了去日内瓦的高能物理会议 , 取消了准备去东南亚的演讲旅行 , 她和她丈夫已经预订了“伊丽莎白王后号”的船票 , 结果她公然放了她丈夫的鸽子 , 让他一个人去日内瓦 , 吴健雄自己留下来做实验 。
吴健雄于满清王朝覆灭那年(1912年)在江苏苏州出生 , 被称为“实验核物理的执政女王” , “东方的居里夫人” , 她参与了曼哈顿计划 , 并成为美国物理学会第一个妇女主席 , 是世界上最杰出的实验物理学家之一 。

本文图片
有如此优秀的吴健雄的鼎力支持 , 实验当然就没什么好担心的了 。 但这里我并不打算给大家讲吴健雄的实验 , 我给大家看一个更简单直观的图像 。 下图就是一个旋转的原子核衰变的时候放出一个电子的图像 , 中间是一面镜子 , 我们从上往下看的时候 , 镜子外的原子核是顺时针方向旋转 , 而镜子里面的原子核是逆时针旋转 。 也就是说 , 一个旋转的原子核的镜像旋转的方向跟它本身旋转方向是相反的 。 物理学家们约定 , 左手顺着旋转的方向 , 大拇指的方向就是原子核旋转的方向 , 所以 , 如箭头所示 , 静止外面的原子核旋转方向向上 , 而镜子里面的向下 。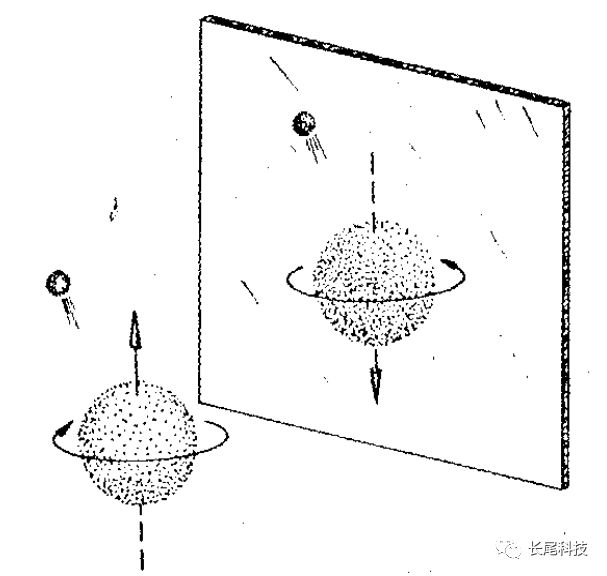
本文图片
我们也很容易想象 , 镜子里外的原子核旋转方向虽然相反 , 但是如果外面的电子往上飞 , 镜子里面的电子也往上飞 , 这很符合常识 , 没什么奇怪的 , 这就是宇称守恒时候的样子 。 但是 , 如果哪天你看到镜子里电子居然是朝下发射的 , 你会不会觉得见鬼了?
当然 , 物理学家说的镜像并不是真的去看镜子 , 镜子无论怎么照肯定都是这样 。 他们的意思是:如果我再找来一个原子核 , 让这个原子核跟镜子里的原子核一模一样(也即是大小质量啥的都相等 , 但是旋转方向不一样) , 我们就说这两个原子核互为镜像 。
然后我再去观察这个镜像原子核 , 如果它跟镜子里一样也是向上发射电子 , 那就不奇怪 , 是宇称守恒;如果它跟镜子里发射电子的方向相反 , 也就是向下发射电子 , 那么宇称就不守恒了 。
当然 , 上面只是理论分析 , 真正要做实验的话 , 有两个难点:第一 , 分子、原子、原子核都在杂乱无章的做热运动 , 你怎么让它跟上图一样安静下来旋转?答案是给它降温 。 温度就是微观粒子热运动的一个表现 , 温度降下来了它们自然就不闹腾了 , 所以吴健雄做实验的时候把温度降到了只比绝对零度(-273.15℃ , 粒子不动的时候的温度 , 无法达到)高0.01K;第二 , 因为微观粒子具有不确定性 , 我不可能去观察一个原子核发射电子的方向 , 我只能观察一堆原子核衰变然后统计他们发射电子方向的概率 。 于是 , 我得让原子核都按照一定的方向旋转 , 这个技术叫原子核的极化 , 这在当时是妥妥的高科技 。
这下子知道为什么说实验的难度巨大了吧 , 不过不管怎样 , 吴健雄完成了实验 , 她测量了一束钴60衰变放出电子的方向 , 证明宇称在弱相互作用下是不守恒的 。 实验结果出来的时候 , 吴健雄自己都不相信这个结果 , 她生怕这是哪里的实验误差导致的 , 于是小心谨慎的再回去检验 。 她也只把初步的实验结果跟杨振宁和李政道说了 , 并且让他们暂时不要对外公布 , 但是 , 显然杨、李二人对这个实验结果并没有那么吃惊 , 于是迫不及待的就告诉别人了 。
消息一出 , 整个物理学界都震惊了!他们立刻去做其他验证宇称守恒的实验 , 结果实验准确无误的显示:在弱相互作用下 , 宇称原来真的不守恒!
本文图片
11宇称不守恒的影响
诺贝尔奖只是宇称不守恒一个很小的注脚 。 杨振宁和李政道在1956年10月发表了《对于弱相互作用中宇称守恒的质疑》的论文 , 吴健雄随后给了实验验证 , 诺组委立马把1957年的诺贝尔奖颁给了35岁的杨振宁和31岁的李政道 。 要知道爱因斯坦在1905年提出来光量子说和狭义相对论 , 1915年完成广义相对论 , 然后诺组委一直拖拖拉拉到1921年 , 也就是爱因斯坦42岁的时候才给颁奖 。
因为宇称不守恒(即便只是在弱相互作用下)并不是一个局部性的理论发展 , 它影响了整个物理学界的方方面面 , 是囊括了分子、原子和基本粒子物理的一个基本革命 。 我在前面花了很大的篇幅给大家介绍了为什么对称性在20世纪物理学里这么重要(对称性对应守恒律) , 特别是爱因斯坦的相对论在时空对称方面取得的巨大成就 , 还有量子力学里对对称性的极度重视 , 使得那时候人们对对称性的信仰和依赖丝毫不比20世纪之前人们对牛顿绝对时空观的依赖弱 。
20世纪初 , 洛伦兹、彭加莱这些人都已经走到狭义相对论的门口了 , 但是就是不愿意放弃牛顿绝对时空的概念 , 因此被年轻的爱因斯坦后来居上 。 20世纪50年代的时候 , 全世界都在为θ-τ之谜绞尽脑汁 , 但是费曼、泡利、朗道这样的物理学大师都不愿意假设宇称不守恒 , 从而让年轻的杨振宁和李政道后来居上 。 他们不愿意放弃宇称守恒 , 因为这些大师们太清楚对称性在物理学的重要程度了 , 而且基于他们的审美观念 , 他们绝不愿意相信上帝会是一个左撇子 。
宇称不守恒的发现震碎了人们对上帝绝对对称的信念 , 迫使人们重新思考对称的问题 , 这一转向导致了后来许多深刻的发现 。 人们慢慢发现 , 上帝虽然喜欢对称 , 但是并不喜欢绝对对称 , 因为绝对对称必然导致大家都一样 , 从而缺乏生机(你想想如果全世界的人都长一个样 , 那将是多么恐怖的一件事) 。 假设宇宙在初期都是绝对对称的 , 那么所有的粒子和相互作用都一样 , 那么怎么会有后来引力、电磁力、强力、弱力的区分呢?所以 , 最开始的对称在一定条件下是会慢慢变成不对称的 , 这样对称就破缺了 , 对称破缺之后就出现了不同的东西 。
比如现在已经知道了的:电磁力和弱力在早期就是完全同一种力 , 叫电弱力 , 后来随着宇宙的环境温度慢慢变化 , 发生了对称性破缺 , 电弱力就分成了现在的电磁力和弱力两种 。 电磁力和弱力的统一是二战后物理学的一个巨大成就 , 统一他们的是一种被称为杨-米尔斯的理论 , 而这个杨-米尔斯里的这个杨 , 正是我们这篇文章的主人公之一的杨振宁 。 其实 , 除了已经完全统一了的电弱相互作用 , 现在用来描述强相互作用的量子色动力学也是一种杨-米尔斯理论 。 正因如此 , 杨-米尔斯方程在现代物理学里极为重要 , 这是继麦克斯韦方程组和爱因斯坦引力场方程之后最为重要的一组方程 。 相比给杨振宁先生了带来诺贝尔奖的宇称不守恒 , 杨-米尔斯方程才是杨振宁先生的最高成就 , 也是东方人在物理学上的最高成就 。

本文图片
_原题_:深度:宇称不守恒到底说了啥?杨振宁和李政道的发现究竟有多大意义?
来源:长尾科技
编辑:前进四
推荐阅读
- 历史|科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 空间|(科技)科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 平板|消息称 vivo 平板明年上半年推出:骁龙 870,四边等宽全面屏设计
- 硬件|汽车之家年底裁员,员工称多个职能部门已被撤销
- ASUS|华硕预热ROG Flow Z13:称其是“全球最强悍的游戏平板”
- 视点·观察|科技巨头纷纷发力元宇宙:这是否是所有人的未来?
- Monarch|消息称微软Win11 2022重大更新将在明年夏天到来
- Apple|法官称苹果零售店搜包和解协议虽不完美,但可继续进行
- IT|报道称Polestar 4电动SUV将跟保时捷Macan电动版对标
- 虚拟|比尔·盖茨关于2022年的五项预言之二:元宇宙成有用的工具







