凝聚态物理中 , 自旋玻璃是一种有随机性的磁量子态 。 我们通常所说的磁自旋 , 一般是三维空间中指向两个磁极的自旋 , 比如说在铁磁性物质中 , 磁自旋指向同一个方向;反铁磁性物质中 , 相邻的自旋会交错朝向相反的方向 。 相比之下 , 自旋玻璃是一种 “无序的” 磁量子态 , 自旋取向随机 , 没有固定模式 , 自旋之间的耦合系数也是随机的 , “玻璃”一词正刻画了这种无序的性质 , 因为日常生活中常见的玻璃是就是典型的非晶体 , 没有晶格结构 , 各种物理性质都区别于晶体 。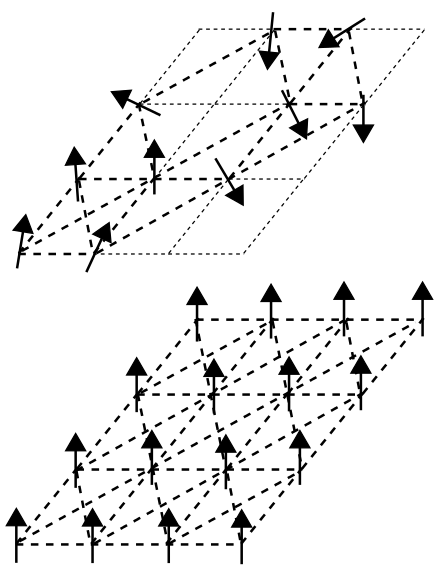
上面为自旋玻璃结构示意图 , 下面为铁磁晶体示意图
图片来自wikipedia词条[6]
自旋玻璃中的原子间耦合(化学键)由大致上相同数目的铁磁键和反铁磁键混合而成 , 相比指向完全有序的体系 , 这种几何上的扭曲被称作受阻挫 。 这种结构带来的结果是 , 自选玻璃的稳态构型并不是最低能量构型 , 因此常常被称为“亚稳态” 。
1975年David Sherrington 和 Scott Kirkpatrick 提出了一个重要的精确可解的自选玻璃模型 , 它的形式是类似于伊辛模型(Ising model)的两体耦合 , 但耦合系数是一个高斯分布 , 且两体不需要是相邻的 , 体系中任意两个自旋都相互耦合 。 随机性和全体-全体相互作用(all-to-all)带来自旋玻璃复杂的结构 。
在1979到1984年的一系列工作中 , Parisi引入了复本对称破缺(replica symmetry breaking)的概念并将其应用到上述自旋玻璃模型(Sherrington-Kirkpartick模型)中去 , 给出了平衡态的解 。 随后的众多作者的一系列工作 , 包括Mezard , Parisi , Virasoro等等 , 发现了阻挫自旋玻璃相的非遍历本质等等性质 。 对这种新物质结构的讨论引发了统计物理中深刻的发展 , 后续在各种无序体系中有广泛的应用 , 例如Replica方法在神经网络的研究中的使用 。
虽然随机过程的研究已经有很深刻的数学体系 , 例如对布朗运动的微分方程描述等 。 但大自然中还有许多概率现象是人们没有理解的 , 比如我们要说的界面增长:最简单的例子就是 , 取一张四方的白纸 , 均匀点燃它朝下的边 , 然后观察燃烧部分和未燃烧部分的边界自下而上地移动 。 又比如 , 一个一维(或者二维)的平台上 , 自天花板不断均匀掉落一些小颗粒 , 这些小颗粒在平台上堆积的表面随着时间流逝而增长(像极了一个大型的俄罗斯方块有木有~) 。
“俄罗斯方块”给出一维的界面增长 。 图片来自Corwin的讲座[5].
推荐阅读
- 数字化|零售数字化转型显效 兴业银行手机银行接连获奖
- 四平|智慧城市“奥斯卡”揭晓!祝贺柯桥客户荣获2021世界智慧城市治理大奖
- 殊荣|蝉联殊荣!数梦工场荣获DAMA2021数据治理三项大奖
- 技术|脉冲+推揉 全能按摩手 SKG G7 Pro颈椎按摩器参加科创奖评选
- 国际|微创血管介入手术机器人获国际创业大赛冠军,获价值千万元奖励
- 机器人|微创血管介入手术机器人获国际创业大赛冠军,获价值千万元奖励
- 最新消息|快手调整员工福利:减少房补、取消免费三餐 新增生育奖金
- 团队|深信院41项科研项目亮相高交会 11个项目获优秀产品奖
- 战略|科力尔电机荣获第一届“新湖南贡献奖先进集体”!
- 最新消息|年终奖计税优惠政策将延续 年前年后到手或差上万元







