这个界面变化的过程 , 数学上可以用一个高度函数来描述 , 这个函数随着时间演化而变化 , 因此是空间坐标和时间的函数 。 Kardar , Parisi和张翼成于1986年提出用如下的偏微分方程来描述[9]: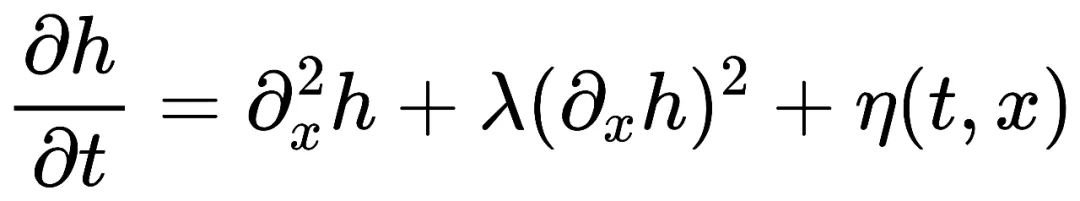
这个过程区别于一般的布朗运动方程的地方在于 , 它是一个非线性方程 , 上面公式中的h对x导数的平方项是非线性的 。 如果我们抛开这个非线性项 , 剩余的部分里
推荐阅读
- 数字化|零售数字化转型显效 兴业银行手机银行接连获奖
- 四平|智慧城市“奥斯卡”揭晓!祝贺柯桥客户荣获2021世界智慧城市治理大奖
- 殊荣|蝉联殊荣!数梦工场荣获DAMA2021数据治理三项大奖
- 技术|脉冲+推揉 全能按摩手 SKG G7 Pro颈椎按摩器参加科创奖评选
- 国际|微创血管介入手术机器人获国际创业大赛冠军,获价值千万元奖励
- 机器人|微创血管介入手术机器人获国际创业大赛冠军,获价值千万元奖励
- 最新消息|快手调整员工福利:减少房补、取消免费三餐 新增生育奖金
- 团队|深信院41项科研项目亮相高交会 11个项目获优秀产品奖
- 战略|科力尔电机荣获第一届“新湖南贡献奖先进集体”!
- 最新消息|年终奖计税优惠政策将延续 年前年后到手或差上万元







