文章图片
表示 t 层隐
藏单元激活向量 , 输入 h_0 = x ,
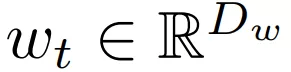
文章图片
表示 t 层的参数 , 在离散设置中
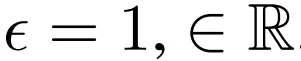
文章图片
该研究通过设置
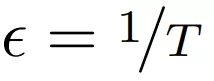
文章图片
并将极限
设为

文章图片
来构建残差网络的连续深度变体 。这样产生一个微分方程 , 该方程将隐藏单元进化描述为深度 t 的函数 。由于标准残差网络每层使用不同的权重进行参数化 , 因此该研究用 w_t 表示第 t 层的权重 。 此外该研究还引入一个超网络(hypernetwork) f_w , 它将权重的变化指定为深度和当前权重的函数 。 然后将隐藏单元激活函数的进化和权重组合成一个微分方程:

文章图片
权重先验过程:该研究使用 Ornstein-Uhlenbeck (OU) 过程作为权重先验 , 该过程的特点是具有漂移(drift)和弥散(diffusion)的 SDE:
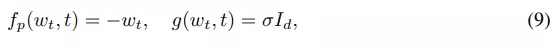
文章图片
权重近似后验使用另一个具有以下漂移函数的 SDE 隐式地进行参数化:
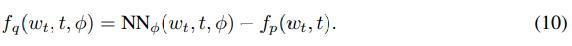
文章图片
然后该研究在给定输入下评估了该网络需要边缘化权重和隐藏单元轨迹(trajectory) 。 这可以通过简单的蒙特卡罗方法来完成 , 从后验过程中采样权重路径 {w_t} , 并在给定采样权重和输入的情况下评估网络激活函数 {h_t} 。 这两个步骤都需要求解一个微分方程 , 两步可以通过调用增强状态 SDE 的单个 SDE 求解器同时完成:
为了让网络拟合数据 , 该研究最大化由无限维 ELBO 给出的边缘似然(marginal likelihood)的下限:
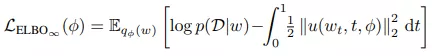
文章图片
采样权重、隐藏激活函数和训练目标都是通过一次调用自适应 SDE 求解器同时计算的 。
减小方差的梯度估计
该研究使用 STL(sticking the landing) 估计器来替换 path 空间 KL 中的原始估计器以适应 SDE 设置:
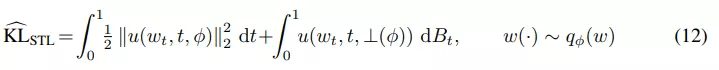
文章图片
等式 (12) 中的第二项是鞅(martingale) , 期望值为零 。 在之前的工作中 , 研究者仅对第一项进行了蒙特卡罗估计 , 但该研究发现这种方法不一定会减少梯度的方差 , 如下图 4 所示 。
推荐阅读
- 网络|天津联通全力助推天津市入选全国首批千兆城市
- 网络化|工信部:2025年建成500个以上智能制造示范工厂
- 视点·观察|张庭夫妇公司被查 该怎样精准鉴别网络传销?
- 数字化|70%规模以上制造业企业到2025年将实现数字化、网络化
- 人物|俄罗斯网络博主为吸引流量 闹市炸毁汽车 结果够“刑”
- 协同|网文论︱网络文学与AI写作:人机协同演化时代的文学之灵
- 周鸿祎|网络安全行业应提升数字安全认知
- 安全风险|网络安全行业应提升数字安全认知
- 海康威视|智能家居战场又添一员,海康威视分拆萤石网络上市,半年营收20亿 | IPO见闻
- 网络应用|免费、不限速 8大网盘今年都已提供无差别速率服务







