文章图片
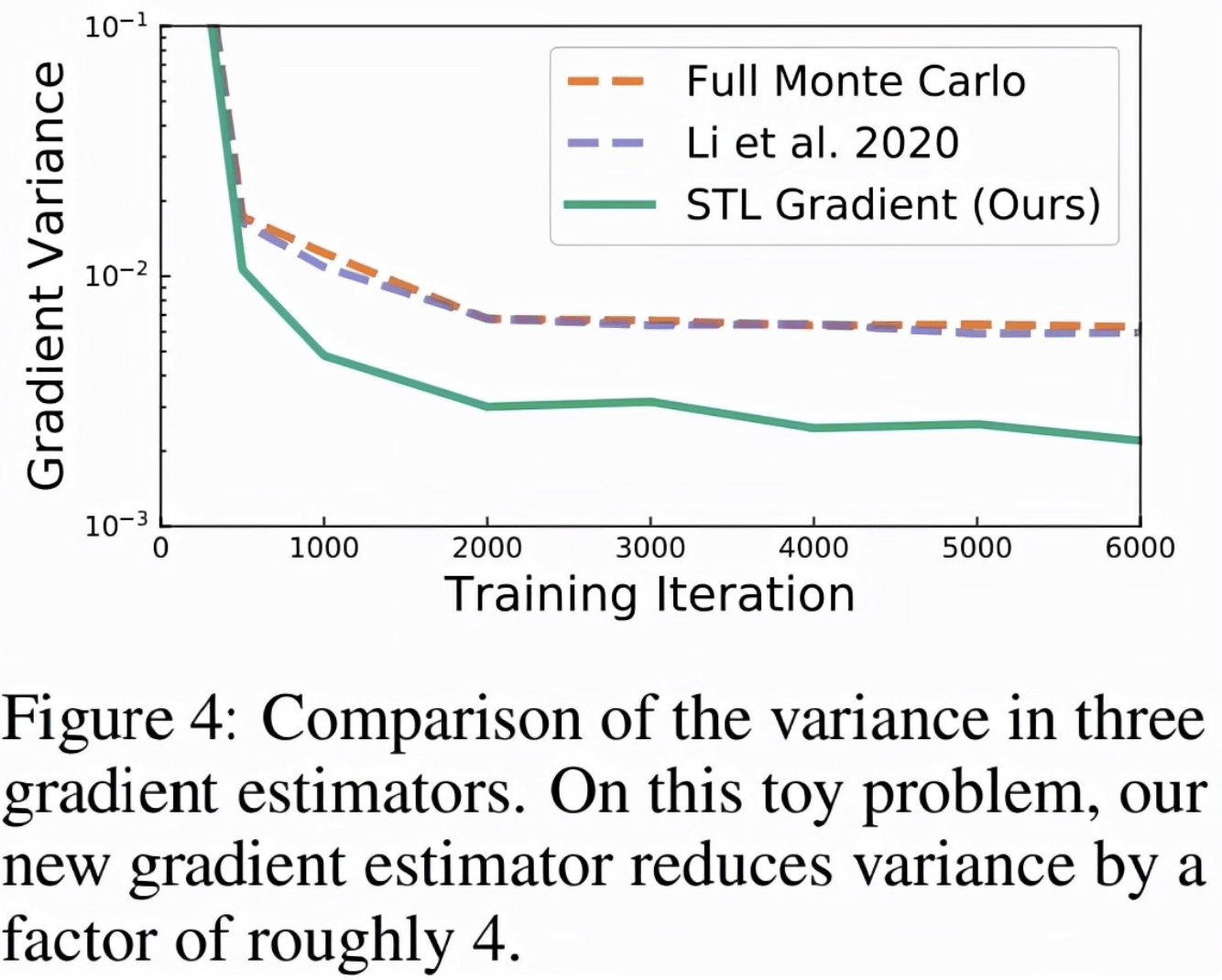
因为该研究提出的近似后验可以任意表达 , 研究者推测如果参数化网络 f_w 的表达能力足够强 , 该方法可在训练结束时实现任意低的梯度方差 。
图 4 显示了多个梯度估计器的方差 , 该研究将 STL 与「完全蒙特卡罗(Full Monte Carlo)」估计进行了比较 。 图 4 显示 , 当匹配指数布朗运动时 , STL 获得的方差比其他方案低 。 下表 4 显示了训练性能的改进 。

文章图片
实验
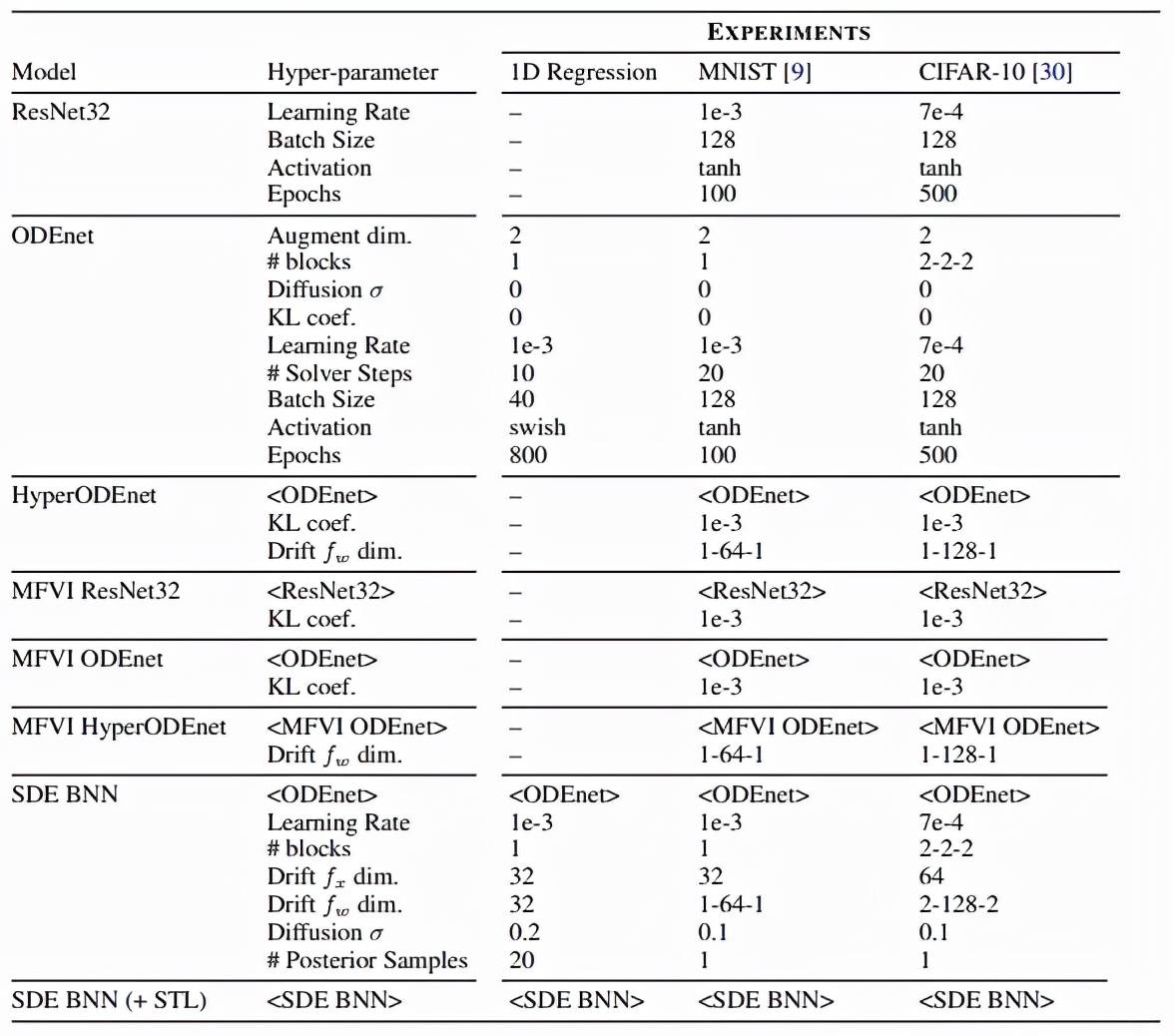
该研究的实验设置如下表所示 , 该研究在 MNIST 和 CIFAR-10 上进行了 toy 回归、图像分类任务 , 此外他们还研究了分布外泛化任务:
文章图片
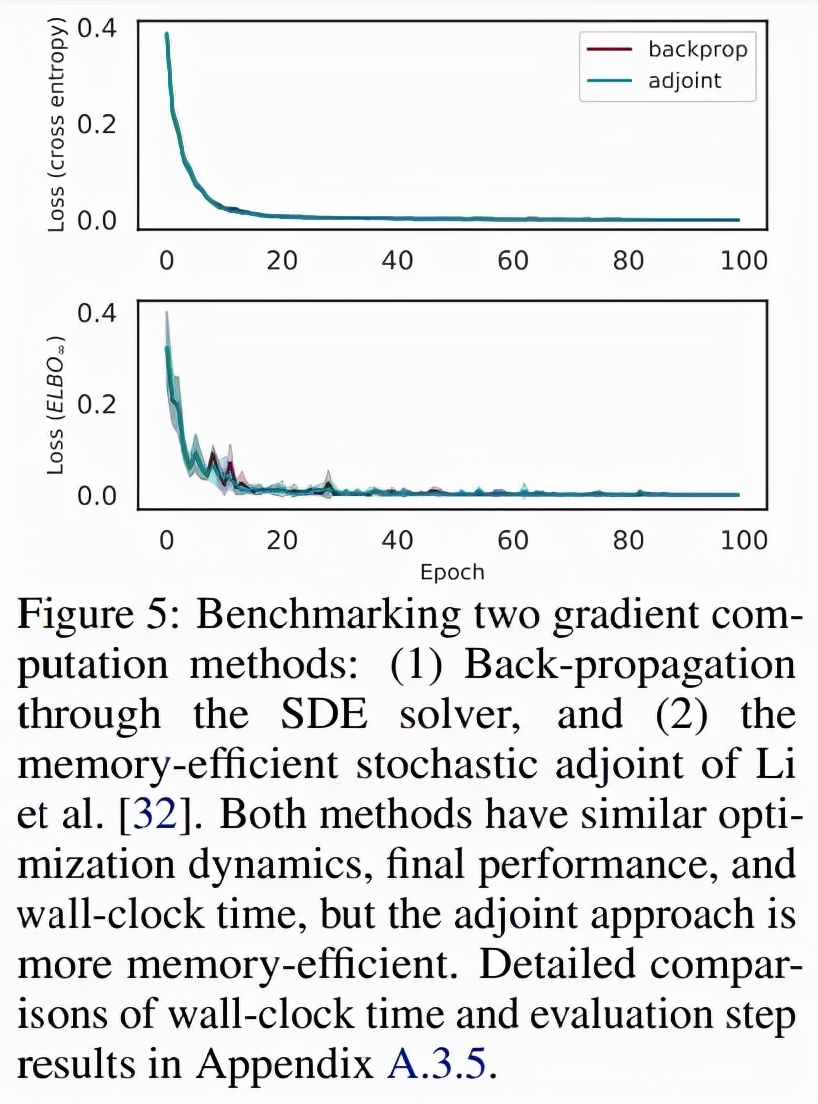
为了对比求解器与 adjoint 的反向传播 , 研究者比较了固定和自适应步长的 SDE 求解器 , 并比较了 Li 等人提出的随机 adjoint 之间的比较 ,图 5 显示了这两种方法具有相似的收敛性:
文章图片
1D 回归
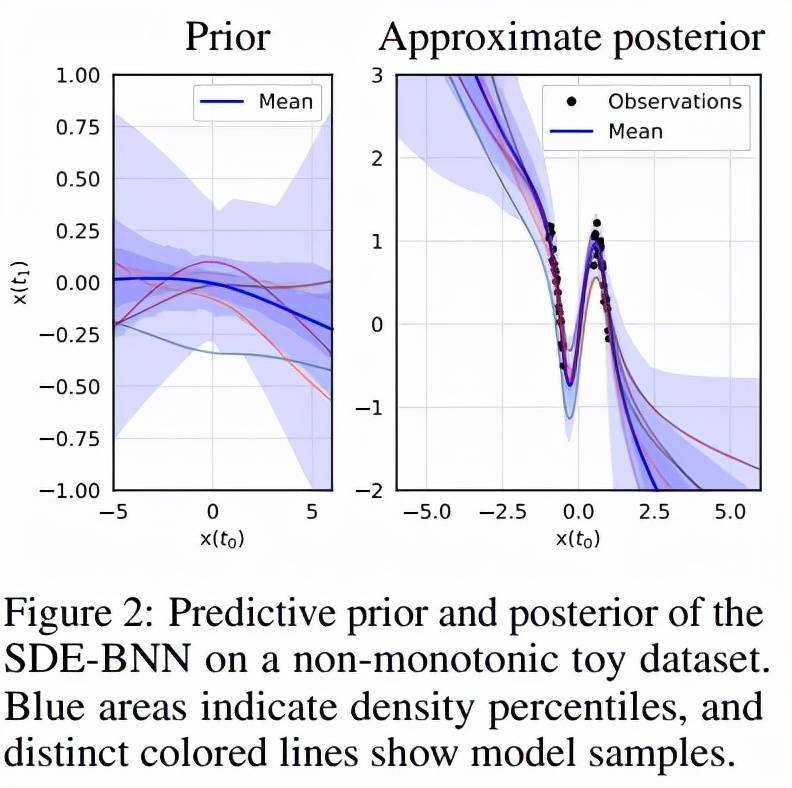
该研究首先验证了 SDE-BNN 在 1D 回归问题上的表现 。 以弥散过程的样本为条件 , 来自 1D SDE-BNN 的每个样本都是从输入到输出的双向映射 。 这意味着从 1D SDE-BNN 采样的每个函数都是单调的 。 为了能够对非单调函数进行采样 , 该研究使用初始化为零的 2 个额外维度来增加状态 。 图 2 显示了模型在合成的非单调 1D 数据集上学习了相当灵活的近似后验 。
文章图片
图像分类
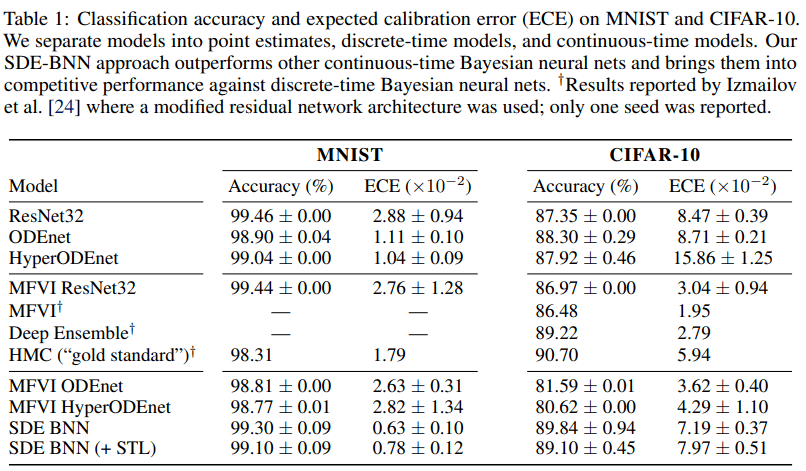
表 1 给出了图像分类实验的结果 。 SDE-BNN 通常优于基线 , 由结果可得虽然连续深度神经 ODE (ODEnet) 模型可以在标准残差网络上实现类似的分类性能 , 但校准(calibration)较差 。
文章图片
图 6a 展示了 SDE-BNN 的性能 , 图 6b 显示具有相似准确率但比神经 ODE 校准更好的结果 。

文章图片
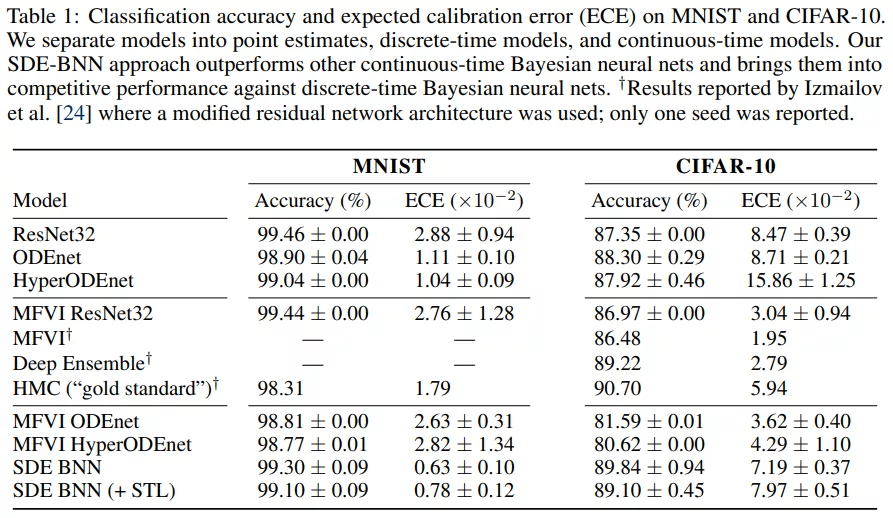
表 1 用预期校准误差量化了模型的校准 。 SDE-BNN 似乎比神经 ODE 和平均场 ResNet 基线能更好地校准 。
文章图片
下图 7 显示了损坏测试集上相对于未损坏数据的误差 , 表明随着扰动严重性级别的增加以及表 1 中总结的总体误差度量 , mCE 稳步增加 。 在 CIFAR10 和 CIFAR10-C 上 , SDE-BNN 和 SDE -BNN + STL 模型实现了比基线更低的整体测试误差和更好的校准 。
推荐阅读
- 网络|天津联通全力助推天津市入选全国首批千兆城市
- 网络化|工信部:2025年建成500个以上智能制造示范工厂
- 视点·观察|张庭夫妇公司被查 该怎样精准鉴别网络传销?
- 数字化|70%规模以上制造业企业到2025年将实现数字化、网络化
- 人物|俄罗斯网络博主为吸引流量 闹市炸毁汽车 结果够“刑”
- 协同|网文论︱网络文学与AI写作:人机协同演化时代的文学之灵
- 周鸿祎|网络安全行业应提升数字安全认知
- 安全风险|网络安全行业应提升数字安全认知
- 海康威视|智能家居战场又添一员,海康威视分拆萤石网络上市,半年营收20亿 | IPO见闻
- 网络应用|免费、不限速 8大网盘今年都已提供无差别速率服务







