易坊好文馆

  1. 首页 > 玩科技 >

模型|17个机器学习的常用算法！( 十 )

问题 数据 进行 算法 样本 分类 包括 方式 模型 公式 vector 分类器 贝叶斯


EM算法：有时候因为样本的产生和隐含变量有关（隐含变量是不能观察的） ， 而求模型的参数时一般采用最大似然估计 ， 由于含有了隐含变量 ， 所以对似然函数参数求导是求不出来的 ， 这时可以采用EM算法来求模型的参数的（对应模型参数个数可能有多个） ，
EM算法一般分为2步：
E步：选取一组参数 ， 求出在该参数下隐含变量的条件概率值；
M步：结合E步求出的隐含变量条件概率 ， 求出似然函数下界函数（本质上是某个期望函数）的最大值 。
重复上面2步直至收敛 ， 公式如下所示：

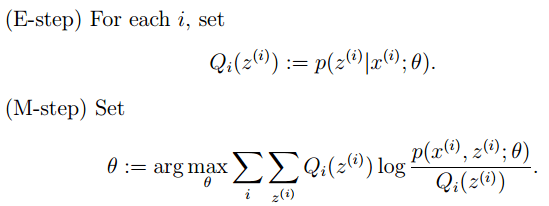
模型|17个机器学习的常用算法！
文章图片

M步公式中下界函数的推导过程：

模型|17个机器学习的常用算法！
文章图片

EM算法一个常见的例子就是GMM模型 ， 每个样本都有可能由k个高斯产生 ， 只不过由每个高斯产生的概率不同而已 ， 因此每个样本都有对应的高斯分布（k个中的某一个） ， 此时的隐含变量就是每个样本对应的某个高斯分布 。
GMM的E步公式如下（计算每个样本对应每个高斯的概率）：
更具体的计算公式为：
M步公式如下（计算每个高斯的比重 ， 均值 ， 方差这3个参数）：

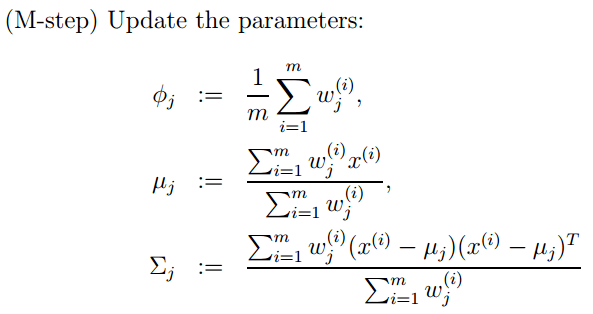
模型|17个机器学习的常用算法！
文章图片

Apriori是关联分析中比较早的一种方法 ， 主要用来挖掘那些频繁项集合 。 其思想是：
1. 如果一个项目集合不是频繁集合 ， 那么任何包含它的项目集合也一定不是频繁集合；
2. 如果一个项目集合是频繁集合 ， 那么它的任何非空子集也是频繁集合；
Aprioir需要扫描项目表多遍 ， 从一个项目开始扫描 ， 舍去掉那些不是频繁的项目 ， 得到的集合称为L ， 然后对L中的每个元素进行自组合 ， 生成比上次扫描多一个项目的集合 ， 该集合称为C ， 接着又扫描去掉那些非频繁的项目 ， 重复…
看下面这个例子 ， 元素项目表格：
如果每个步骤不去掉非频繁项目集 ， 则其扫描过程的树形结构如下：

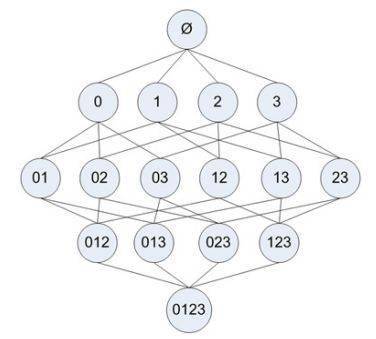
模型|17个机器学习的常用算法！
文章图片

在其中某个过程中 ， 可能出现非频繁的项目集 ， 将其去掉（用阴影表示）为：

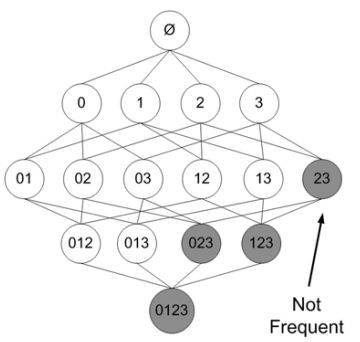
模型|17个机器学习的常用算法！
文章图片

FP Growth是一种比Apriori更高效的频繁项挖掘方法 ， 它只需要扫描项目表2次 。 其中第1次扫描获得当个项目的频率 ， 去掉不符合支持度要求的项 ， 并对剩下的项排序 。 第2遍扫描是建立一颗FP-Tree(frequent-patten tree) 。

推荐阅读


上一篇：英国殖民地|英国女王，被辞退了｜地球知识局

下一篇：功能|真正全能型体验——荣耀平板V7 Pro 体验