易坊好文馆

  1. 首页 > 玩科技 >

模型|17个机器学习的常用算法！( 七 )

问题 数据 进行 算法 样本 分类 包括 方式 模型 公式 vector 分类器 贝叶斯


下面通过一个例子来简单说明 ， 假设的是5个训练样本 ， 每个训练样本的维度为2 ， 在训练第一个分类器时5个样本的权重各为0.2. 注意这里样本的权值和最终训练的弱分类器组对应的权值α是不同的 ， 样本的权重只在训练过程中用到 ， 而α在训练过程和测试过程都有用到 。
现在假设弱分类器是带一个节点的简单决策树 ， 该决策树会选择2个属性（假设只有2个属性）的一个 ， 然后计算出这个属性中的最佳值用来分类 。
Adaboost的简单版本训练过程如下：
1. 训练第一个分类器 ， 样本的权值D为相同的均值 。 通过一个弱分类器 ， 得到这5个样本（请对应书中的例子来看 ， 依旧是machine learning in action）的分类预测标签 。 与给出的样本真实标签对比 ， 就可能出现误差(即错误) 。 如果某个样本预测错误 ， 则它对应的错误值为该样本的权重 ， 如果分类正确 ， 则错误值为0. 最后累加5个样本的错误率之和 ， 记为ε 。
2. 通过ε来计算该弱分类器的权重α ， 公式如下：

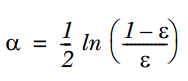
模型|17个机器学习的常用算法！
文章图片

3. 通过α来计算训练下一个弱分类器样本的权重D ， 如果对应样本分类正确 ， 则减小该样本的权重 ， 公式为：

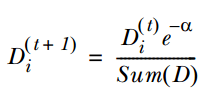
模型|17个机器学习的常用算法！
文章图片

如果样本分类错误 ， 则增加该样本的权重 ， 公式为：

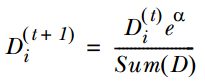
模型|17个机器学习的常用算法！
文章图片

4. 循环步骤1,2,3来继续训练多个分类器 ， 只是其D值不同而已 。
测试过程如下：
输入一个样本到训练好的每个弱分类中 ， 则每个弱分类都对应一个输出标签 ， 然后该标签乘以对应的α ， 最后求和得到值的符号即为预测标签值 。
Boosting算法的优点：
1. 低泛化误差；
2. 容易实现 ， 分类准确率较高 ， 没有太多参数可以调；
3. 缺点：
4. 对outlier比较敏感；
聚类：
根据聚类思想划分：
1. 基于划分的聚类:
K-means, k-medoids(每一个类别中找一个样本点来代表),CLARANS.
k-means是使下面的表达式值最小：

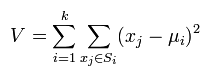
模型|17个机器学习的常用算法！
文章图片

k-means算法的优点：
（1）k-means算法是解决聚类问题的一种经典算法 ， 算法简单、快速 。
（2）对处理大数据集 ， 该算法是相对可伸缩的和高效率的 ， 因为它的复杂度大约是O(nkt) ， 其中n是所有对象的数目 ， k是簇的数目,t是迭代的次数 。 通常k<<n 。 这个算法通常局部收敛 。
（3）算法尝试找出使平方误差函数值最小的k个划分 。 当簇是密集的、球状或团状的 ， 且簇与簇之间区别明显时 ， 聚类效果较好 。

推荐阅读


上一篇：英国殖民地|英国女王，被辞退了｜地球知识局

下一篇：功能|真正全能型体验——荣耀平板V7 Pro 体验