|切与割有什么区别？到底什么是切线？切点真的是一个点吗？( 八 )_

$f'(c)$ ，则称直线为曲线在点 $x=c$ 处的切线。
根据这个定义，只要知道曲线的函数表达式，就可以通过求导的方法得到曲线在任一点的切线的斜率，加上这个已知点，我们就能唯一的将切线确定下来。
当然，对于非光滑的曲线，由于在某些位置，导数是不存在的，因此切线也就不存在了。
莱布尼兹关于切线的定义里，蕴含了他的微分思想。
学过微分的都知道，微分是无限趋近于零，但却不等于零的值。这保证了两个点还是两个点，只是彼此无限靠近！这一点非常重要。
因此，切线是曲线上无限接近，但又没有完全重合的两点决定的一条直线。
这个定义与大多数人心目种的切线定义不同，很多人往往认为切点是一个点，其实你想想，一个点怎么能确定一条直线呢？必须要两个点啊！
所以，切点从本质上讲包含两个点，两个无限靠近的点。
呃，是不是有点被颠覆世界观的的感觉？切点不就是一个点嘛，怎么会是两个点？
是的，如果你只是关心位置，那么切点就是一个点，它就是那个不动的点蜕变而来的。但只是在那个动点无限靠近时，它才转正成为切点！在此之前，它不是切点。
所以，莱布尼兹的定义是多么美妙！
而莱布尼兹的定义与阿波罗尼奥斯的定义是一致的，下面动画清楚的显示这一点：你无法在切线与曲线形成的角里再插入一条直线。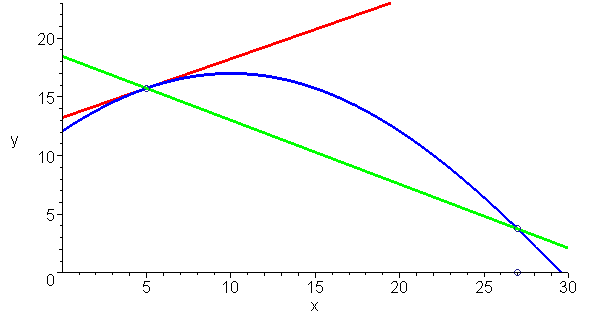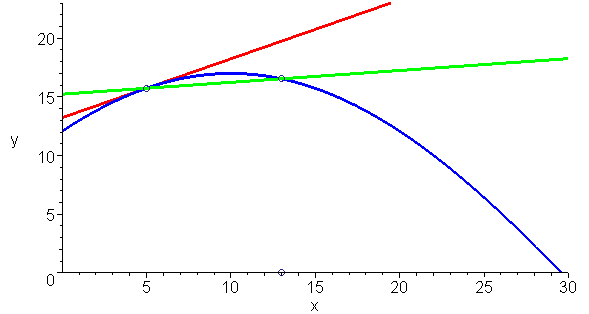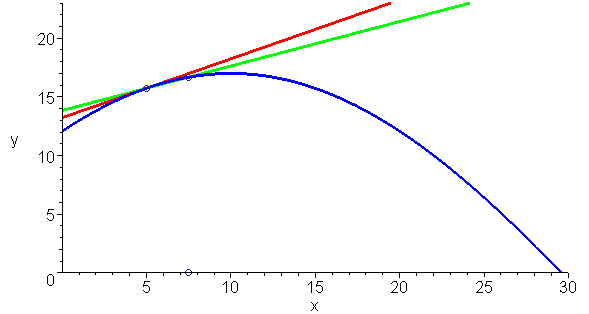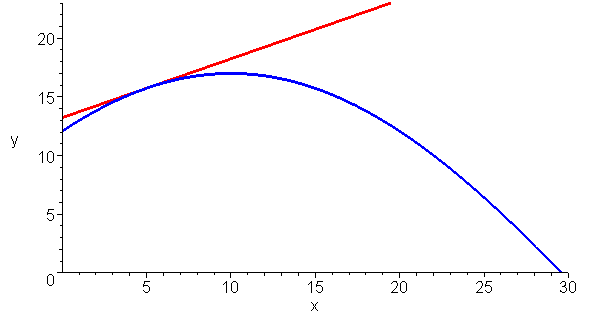

本文图片

最后再来看一个问题：曲线上任一点是否只有一条切线呢？
很多人的答案是肯定的，并且在学习电场时，还据此来理解电场线为什么不能相交的问题。但恐怕很多人在这个问题上有点逻辑颠倒。实际上，电场线不能相交，那是因为任一点场矢量的方向是唯一确定的，并不能说明曲线上每点只能有一条切线！