文章图片
文章图片
【λ/8分辨率的高保真远场显微镜】
文章图片
本文基于λ/8分辨率的高保真远场显微镜的研究 。
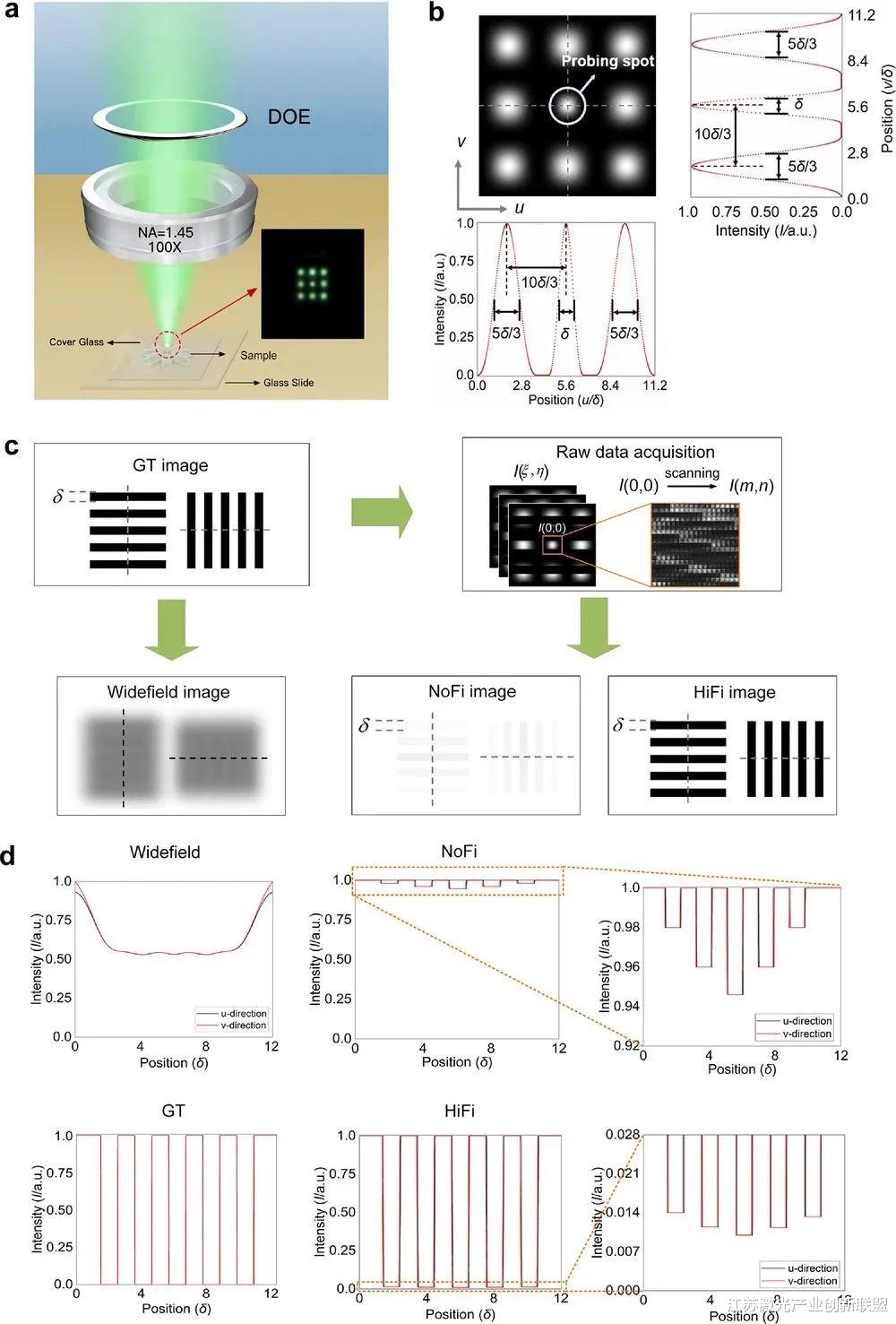
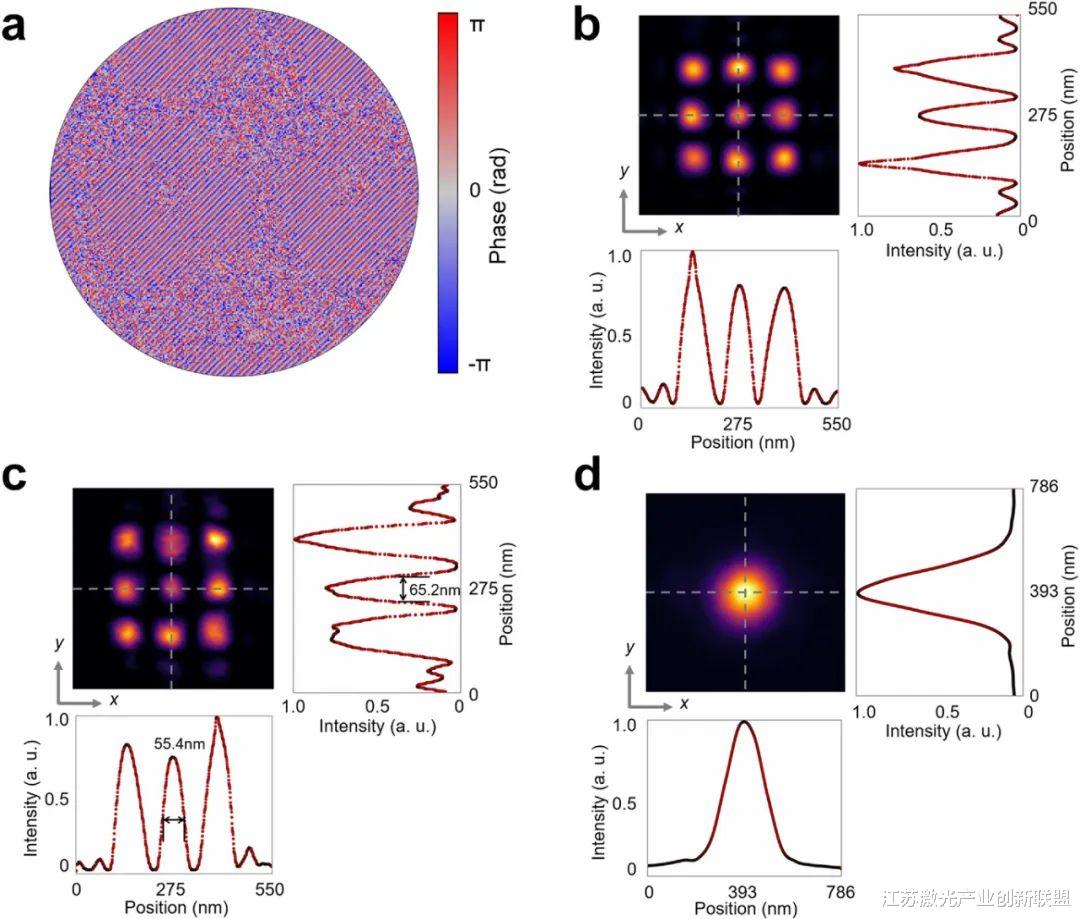
摘要:远场超分辨率显微镜的出现为纳米级成像带来了新的可能性 。 利用点扫描实现远场超分辨率的方法通常依赖于在空间上减小聚焦光斑的大小 。 然而 , 聚焦光斑总是以探测主瓣和高强度副瓣极低的光效率为代价获得高分辨率 , 这限制了在纳米级成像中的应用 , 并可能导致样品的误译 。 在二维多层衍射光学元件(DOE)的辅助下 , 实现了一个衍射效率为3.76%、分辨率为艾里光斑尺寸38%的尖锐探测光斑 。 通过突破圆形0 -π二元结构超振荡透镜的限制 , 使DOE的衍射效率在相同分辨率下提高了至少两个数量级 。 为了消除高强度旁瓣的影响 , 基于改进的反褶积算法 , 利用先验知识对高保真图像进行重构 。 最后 , 构建了高保真远场显微镜(HiFi-FM) , 实验结果表明 , 在获得高保真的同时 , HiFi-FM对空间复杂样品的分辨率优于69 nm 。
1简介
微观系统的经典判据表明 , 基本分辨率受光束波长λ的限制 , 数值孔径(NA)将横向空间分辨率限制在200 nm左右 。 为了观测纳米尺度的物体 , 光学研究人员不遗余力地通过提高光学传递函数(OTF)的空间频率响应或提高OTF的截止频率来实现远场超分辨率成像 。 例如 , 结构照明显微镜增加了OTF的截止点 , 共聚焦显微镜提高了OTF的空间频率响应 。 减小聚焦光斑的尺寸是改善OTF空间频响最有希望的方法之一 。
正如最初由Toraldo di Francia提出的 , 聚焦超出阿贝-瑞利衍射极限可以通过瞳孔滤波技术实现 。 研究了用超振荡透镜和衍射光学元件(DOE)生成紧聚焦光斑的方法 , 并对样品图像进行了点对点重建 , 在一定条件下 , 分辨率可达λ/6.[20
值得注意的是 , 微球增强光学成像技术近年来也得到了广泛的发展 , 以克服衍射极限 。 高分辨率成像的持续挑战仍然要求在实践中提高空间分辨率 。
虽然取得了这些进展 , 但探测点的衍射效率极低和高强度晕限制了其应用前景 。 通常 , 报道的圆形0–π二元结构超振荡透镜对于30%艾里光斑分辨率的效率远远小于0.01% 。 用0 -π超振荡透镜分析表明 , 当聚焦光斑尺寸小于0.38λ/NA时 , 聚焦光斑不可避免地存在旁瓣 。
此外 , 由于高强度光晕的影响 , 超分辨率成像的保真度也受到了挑战 。 在一点一点的情况下 , 许多研究者关注如何减小主瓣宽度以提高分辨率 。 然而 , 聚焦斑旁瓣的强度和分布对最终重建的超分辨率图像有影响 。 特别是 , 使用超分辨率技术发现的生物结构需要用高保真度(HiFi)来解释 , 以避免误解 。 一些研究人员一直致力于开发重建算法 , 包括迭代反褶积和将点扩散函数(PSF)设计成理想形式 。 然而 , 逐点重建算法很少用于实现HiFi超分辨率图像 。
在这里 , 我们提出并实验证明了一种高保真远场显微镜(HiFi-FM) , 可以重建空间分辨率为λ/8的超分辨率复杂图像 。 与圆形二元超振荡透镜相比 , 二维多级DOE提高了探测光斑的效率 。 在分辨率为艾里光斑尺寸38%的情况下 , 我们生成了一个锐利的探测光斑 , 效率为3.76% , 比相同分辨率下的超振荡透镜效率至少提高了两个数量级 。 在此基础上 , 提出了一种基于先验知识的改进反褶积算法的超分辨率重建算法 。 对于空间复杂的样品 , HiFi-FM可获得69 nm的高保真空间分辨率 , 并与宽视场和非保真(NoFi)重建结果进行了比较 。
2原理
2.1 HiFi-FM理论与演示
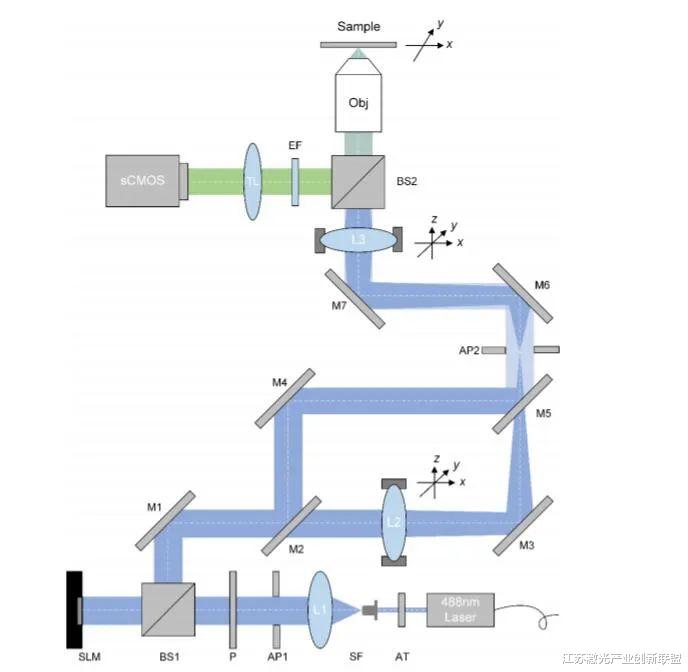
HiFi-FM的原理如图1a所示 。 该系统由两个部分组成:照明系统(蓝色射线 , 见图S1 , 辅助信息)和成像系统(绿色射线 , 见图S1 , 辅助信息) 。 具体来说 , DOE (xy平面 , DOE平面)与照明物镜产生的聚焦光斑在样品(uv平面 , 傅里叶平面)中衍射 。 样品被紧密聚焦的点扫描 , 称为探测点 , 需要进行奈奎斯特-香农采样以获得超分辨率信息 , 周围的其他8个点称为约束点 , 以协助生成探测点 。 探测点与约束点之间存在明显的暗区 。 成像系统可获得探测器上的强度值I(ξ ,η)(来自样品的荧光或非荧光) , I(00)值对应探测点的中心 。 扫描时可以得到I(m n)(00)的离散值 , 用于生成超分辨率图像 , 这里下标(m n)表示探测点的扫描位置 。 为了简化 , I(m n)(00)被写成I(m n) 。 第3.4节和图S1(支持信息)给出了实验几何的完整描述 。
推荐阅读
- 抗原检测颜色越深病毒量越高吗?是否还会“二次感染”?
- AbMole科研-用于MR分子和化学放射增敏的\卵黄壳\样纳米系统的快速合成
- 胜过孙悟空“火眼金睛”的仪器—显微镜
- 一加11还有流浪地球联名款?行星发动机版未发先火,期待值已拉满
- 地球文明循环证据被发现?俄渔民意外打捞出2.5亿年前的高科技物品,引发轰动
- 时间旅行可能吗?
- 学习院士王承书弘扬科学家精神ppt
- 微小的金属雪花展示了新的纳米级制造方法
- 狗狗绝育意外去世,主人:医生跪下给狗道歉!







