|切与割有什么区别？到底什么是切线？切点真的是一个点吗？( 三 )_

1828年之后，词典里对切线的给出的定义是：
切线指的是一条刚好触碰到曲线上某一点的直线。
实际上， “切线”一词的英文——“tangent” ，源自拉丁语“to touch” ，表示接触的意思。窃以为，这种接触就是点到为止，不过分依靠和攀附。
据此描述，对于将切线演示出来这件事，具有良好的可操作性：当你拿着一根不太长的直线靠近曲线上的某个确定点时，只要让你手里的直线与曲线刚好接触，你手里的直线就是那条要找的切线。
若你将一根刚性直杆搭在一个圆球上，只要你避免杆的两端与球面直接接触，可以肯定，杆必定与球保持相切。
如下图，假设地面光滑，左边的球与墙壁接触但无压力，因此球没有发生形变，所以墙面和球面刚好接触，二者相切。而右边的球因为受到细线的斜拉力，必定受到墙面的支持力，球面发生形变，它与墙之间并非点到为止，因此墙面不是球面的切面。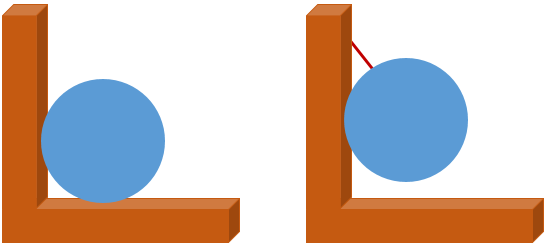

本文图片

虽然这种切线定义是正确的，并且实际操作性强。但这句话有点模糊， “刚好触碰”什么意思？感觉正经的数学定义不会这么说，的确不太好理解，所以这个定义的接受度不是很高。
为了解决广大群众对数学知识的向往与有限的理解力之间的矛盾，人们需要一种更浅显的说法。比如：有几个交点就算切线？于是， “只交于一点”这么一个最直观，但却很容易找到反例的错误说法依然占有较大的市场。
难道在漫长的人类文明史中，切线的定义就只是这个？
非也！太小看历史上的那些聪明的数学家了！其实早在古希腊时代，人们就给出了准确的定义，后来人们又对切线给出多种定义。但遗憾的是，或许是因为数学和几何上的严格定义往往是比较抽象的，这些正确定义并未被大众所熟知。
那么，到底有哪些大牛曾经提出过正确的切线的定义呢？其实，古希腊的数学家欧几里德和阿基米德、比牛顿稍早的法国数学家费马以及牛顿本人等，都对切线做过研究。本文无意去地毯式探求切线定义的发展历史，只列举一下最为重要的两个定义。
第一个定义来自古希腊三大数学家之一的阿波罗尼奥斯（Apollonius of Perga ，约公元前262～190）。

本文图片

在数学中，喇叭角，也称为horn angle ，是一种曲线角，定义为两条相切的曲线之间形成的角。下面这只牛角表面沿纵向正对的两条曲线近似牛角尖处相切，因此就形成一个喇叭角。当然，你可能会钻牛角尖，因为牛角是个立体角。